「データ分析に興味はあるけれど、“変数”って何?」「ヒストグラムってどう使うの?」
そんな疑問を持っている方へ——この記事では、統計学の基本である変数の分類と、ヒストグラムや累積分布グラフによるデータの可視化について、初心者にもわかりやすく解説します。
「名義尺度」「順序尺度」「間隔尺度」「比率尺度」といったキーワードを丁寧に説明し、最後には実際の表やグラフを使って統計の基本を体験できる内容となっています。
初めて統計を学ぶ方にこそ読んでほしい、入門ガイドです!
変数
まず、変数をどのように分類するかについて説明します。
統計において、変数は分析の主な対象です。ですから、まずは変数の種類を整理しましょう。
変数とは何かを理解する助けとして、サンプルデータを含む表を用意しました。
| 州 | 平均気温(°F) | 人口(百万人) |
|---|---|---|
| カリフォルニア | 65 | 39.5 |
| テキサス | 70 | 29.0 |
| フロリダ | 75 | 21.5 |
| ニューヨーク | 55 | 19.5 |
| イリノイ | 52 | 12.5 |
| ペンシルベニア | 50 | 12.8 |
| オハイオ | 51 | 11.7 |
| ジョージア | 68 | 10.7 |
この表では、”行”が「表側」と呼ばれ、アメリカの州を示しています。また”列”が、「表頭」と呼ばれ、州名、平均気温(華氏)、人口が記載されています。
では、この表における変数は何でしょうか?
この表では、各列が1つの変数を表しています。たとえば「州名」「平均気温(華氏)」「人口」などです。
変数の分類
次に、これらの変数を整理・分類してみましょう。
変数は、4つの尺度(スケール)に基づいて分類されます。
これらの尺度は、データを測る「物差し」のようなものだと考えてください。
4つの尺度は以下のとおりです:
- 名義尺度(Nominal Scale)
- 順序尺度(Ordinal Scale)
- 間隔尺度(Interval Scale)
- 比率尺度(Ratio Scale)
名義尺度(Nominal Scale):
まずは名義尺度から始めましょう。
この尺度では、値が「同じか異なるか」だけが意味を持ちます。
例には、性別(男性/女性)や職業(会社員/自営業)などがあります。
これらの値には順序やランク付けはありません。
順序尺度(Ordinal Scale):
次は順序尺度です。
ここでは、「同じか異なるか」に加えて、「順番」も意味を持ちます。
たとえば、A・B・Cのような評価ランクには順番があります。
「不満・普通・満足」のような満足度のレベルにも意味のある順番があります。
間隔尺度(Interval Scale):
さらに進むと、値の差が意味を持つようになります。これを間隔尺度と呼びます。
良い例が気温です。
10度と11度の差は、11度と12度の差と同じ意味を持ちます。
このように、間隔が均等で意味のある場合、気温は間隔尺度の変数とされます。
比率尺度(Ratio Scale):
最後に、比率尺度は「順序」「間隔」に加えて、「値の比率」にも意味がある変数です。
つまり、これらの変数には真のゼロ点があり、そのゼロを基準として値を比例的に解釈できます。
例としては、長さ、重さ、価格などがあります。
たとえば「10cmは5cmの2倍の長さ」、「200円は100円の2倍の価格」というようにです。
一方で、気温のような間隔変数においては、「20°Cは10°Cの2倍暑い」とは言いません。
なぜなら、ゼロが「完全な無」を意味していないからです。
このように、比率の解釈ができるかどうかが、間隔尺度と比率尺度の大きな違いです。
まとめ:4つの尺度の概要
- 名義尺度・順序尺度の変数は「質的変数」と呼ばれます。ラベルやタグのようなもので、定規では測れません。
- 間隔尺度・比率尺度の変数は「量的変数」と呼ばれます。定規やスケールで測る実際の値です。
- 間隔尺度は「均等な目盛りのある定規」、
- 比率尺度は「真のゼロを持つ定規」と考えるとわかりやすいです。
| カテゴリ | 尺度 | 説明 | 例 |
|---|---|---|---|
| 質的 | 名義尺度 | 自然な順序のないカテゴリー | 性別(男/女)、血液型(A/B/O) |
| 質的 | 順序尺度 | 意味のある順序があるが、間隔は均等でない | 評価(優/良/可)、満足度(高/中/低) |
| 量的 | 間隔尺度 | 等間隔の数値。真のゼロがない | 気温、西暦年(例:1990年) |
| 量的 | 比率尺度 | 等間隔かつ真のゼロを持ち、比率が意味を持つ | 身長、体重、人口 |
ヒストグラムと累積分布(量的変数)
続いて、ヒストグラムについて見ていきましょう。
これは、先ほどの量的変数の分布を視覚化するためのツールです。
ヒストグラムと累積分布とは?
ヒストグラムと累積分布は、量的変数の値がどのくらい頻繁に出現するか、つまり変数の分布を理解するためのグラフです。
これらを描くには、「度数分布表」と呼ばれるものを使います。以下の例をご覧ください:
| 年齢層 | 人数(百万人) | 相対度数(%) | 累積相対度数(%) |
|---|---|---|---|
| 10歳未満 | 8.0 | 9.64 | 9.64 |
| 10〜19歳 | 8.5 | 10.24 | 19.88 |
| 20〜29歳 | 7.0 | 8.43 | 28.31 |
| 30〜39歳 | 10.0 | 12.05 | 40.36 |
| 40〜49歳 | 11.0 | 13.25 | 53.61 |
| 50〜59歳 | 12.0 | 14.46 | 68.07 |
| 60〜69歳 | 11.0 | 13.25 | 81.33 |
| 70〜79歳 | 9.0 | 10.84 | 92.17 |
| 80歳以上 | 5.5 | 6.63 | 98.80 |
| 不明・その他 | 1.0 | 1.20 | 100.00 |
少し複雑なので、注意して見ていきましょう。
この場合、「年齢」という量的変数をいくつかのクラス(区間)に分けて、それぞれの人数(度数)をカウントしています。
つまり、これは「年齢」という変数に関する度数分布表です。
表を読むには、「10歳未満の人数は800万人」「20代は700万人」などと解釈します。
ヒストグラムとは?
この度数分布表に基づくヒストグラムは下図のようになります。
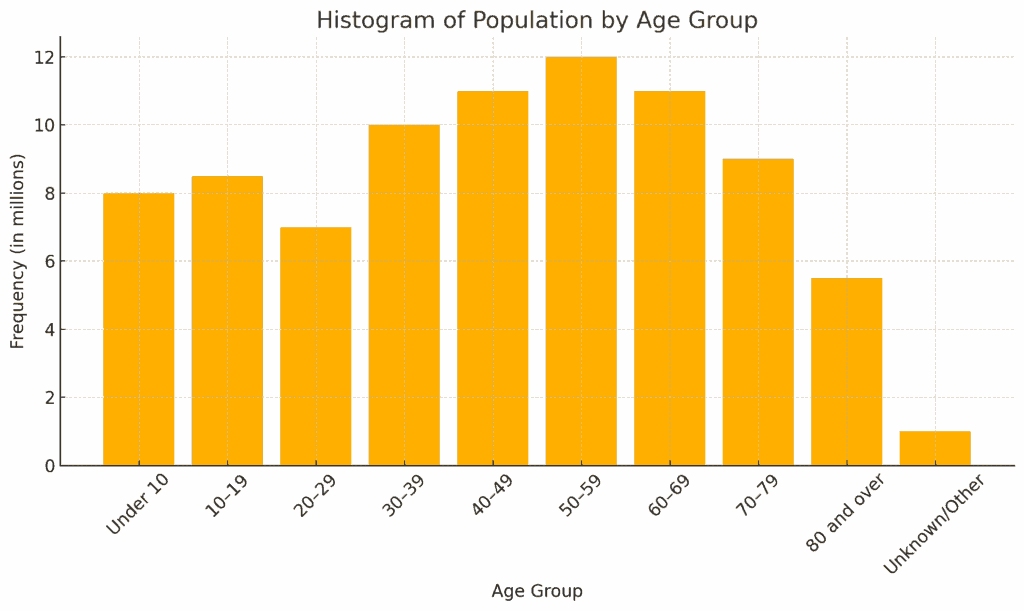
重要なポイントは、変数の分布を調べるためのグラフなので、
- 横軸:変数(ここでは年齢)
- 縦軸:各クラスの度数(人数)
となります。
このヒストグラムでは、横軸が「年齢」、縦軸が「各年齢層の人口(百万人単位)」を表します。
こうして、人口の分布が一目で分かるようになります。
累積分布とは?
ヒストグラムが各グループの出現頻度を示すのに対し、累積分布は「これまでにどれだけ蓄積されたか」を示します。
「ここまででどれだけ到達したか」が分かるのです。
これは、時間やカテゴリーを通じての増加や累積を示し、「50%達成」「80%到達」といったマイルストーンも視覚的に確認できます。
累積分布の描き方
累積分布を描くには、まず「相対度数」を求めます。
相対度数とは、全体を100%としたとき、各クラスがどれだけの割合を占めているかを表します。上の表では3列目が相対度数ですね。
例として、10歳未満が800万人であれば、その相対度数は9.64%となります。
これを小さいクラスから順に加算(累積)していくと、「累積相対度数」が得られ、それに基づいて累積分布グラフを描くことができます。
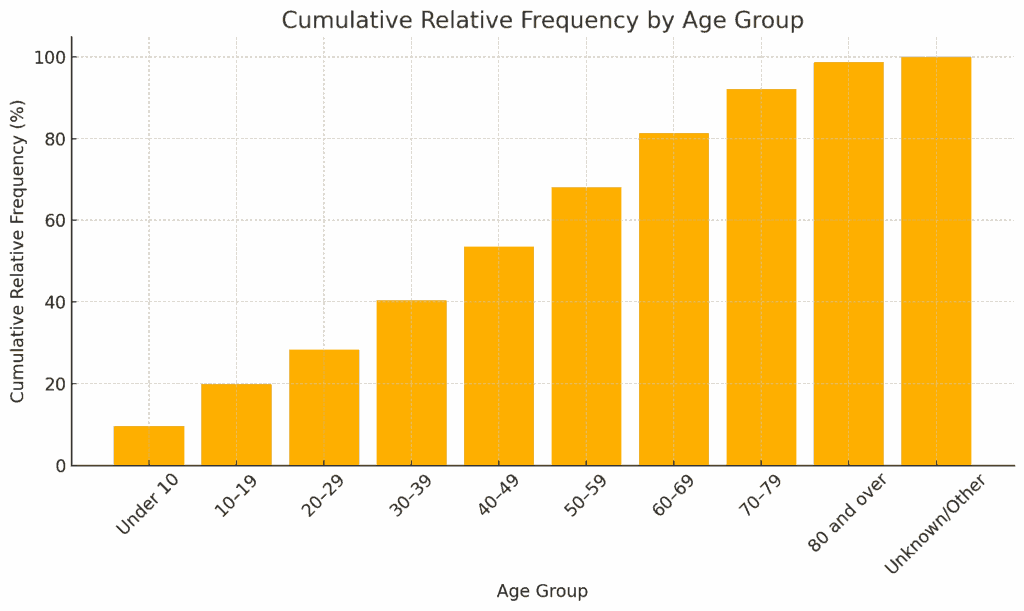
累積分布グラフの見方
上記グラフでは、横軸は「年齢」、縦軸は「累積相対度数」となります。
ヒストグラムではクラスごとの値を個別に示しますが、累積分布グラフでは、それぞれのクラスまでの累積された割合を確認できます。
たとえば、累積相対度数が50%に達するのは「40〜49歳」の年齢層にあたります。
これは、人口の約半分が50歳未満であることを意味しています。
まとめ
この記事では、記述統計の基礎として:
- 変数の分類方法
- 名義・順序・間隔・比率という4つの尺度
- ヒストグラムと累積分布という可視化ツール
について学びました。

変数の種類を理解することで、分析に適した方法を選ぶことができます。そして、度数分布表やヒストグラムはデータのパターンをより明確に示してくれます。さらに累積分布を使えば、その「蓄積の過程」も可視化できます。
これらは、統計やデータ分析を学び始めるすべての人にとって、不可欠な基礎知識ですので、しっかりと理解しておいてくださいね。




コメント