
「正規分布」という言葉は、統計学を学んでいる人なら必ず耳にする言葉ですね。
多くの方が正規分布といえば、下の図のように釣鐘状のカーブを描き、左右対称っていうところまでは、イメージがつくと思います。
正規分布の特徴
正規分布の基本的な特徴として:
- 釣鐘形
- 左右対称
- 平均と中央値が中央で一致している
が挙げられます。さらに、この正規分布図では、「平均」と「分散」が重要となります。
- 平均(\(μ\)):分布の中心の位置を決める
- 分散(\(σ^2\)):どれくらい平均から離れて分布していかを決める
正規分布は \(N(μ, σ^2)\) と表記され、N(normal distribution)は平均\(μ\)と分散(\(σ^2\))に従うことを表しています。
つまり、正規分布は平均と分散(もしくは標準偏差)により分布が決まります。下図では平均が50、標準偏差の違いにより、正規分布が異なることが分かりますね。
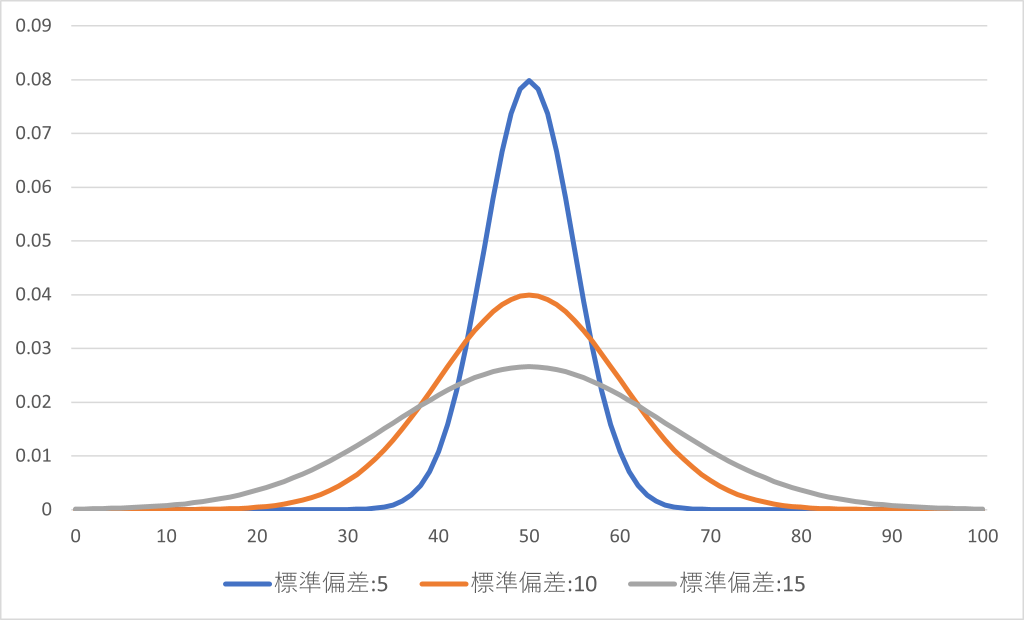
分散(もしくは標準偏差)が小さいと分布は平均の周りに集中し、分散(もしくは標準偏差)が大きいと分布が広がります。
正規分布と標準偏差
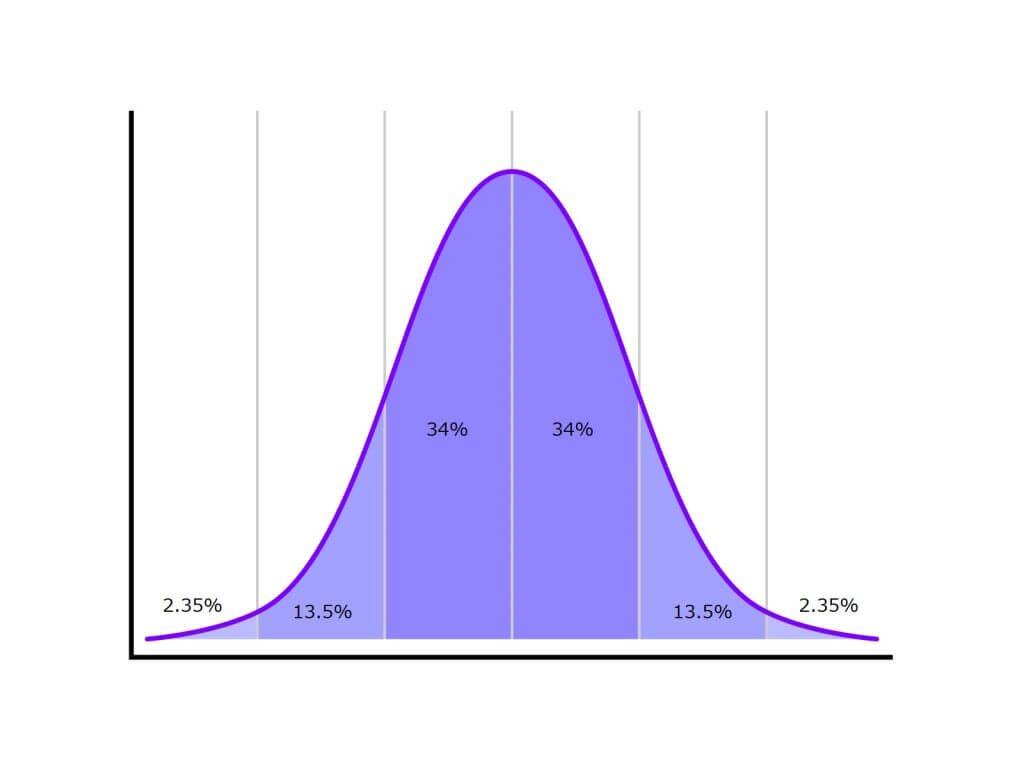
統計学のEmpirical ruleとして、「正規分布の68‐95‐99ルール」というのがあります。
これは、
- 約68%のデータは±1標準偏差内
- 約95%のデータは±2標準偏差内
- 約99%のデータは±3標準偏差内
に含まれるというものです。
Rを使った正規分布
Rを使えば、正規分布も簡単に扱うことができます。正規分布は”norm”を使います。IQを例に解説していきますね。
(※IQは平均値:100、標準偏差:15です)
確率密度関数はdnorm関数
正規分布の確率密度関数の公式は以下のようにややこしいですね。
$$f(X) = \frac{1}{\sqrt{2πσ^2}}\exp{[-\frac{(x-μ)^2}{2σ^2}]}$$
でも、Rのdnorm関数を使えば簡単です。例えば、IQが110の確率密度関数を計算する場合、
dnorm(110, mean = 100, sd = 15)
[1] 0.02129653
となります。
注意!
dnorm関数の結果は確率密度関数です。「確率密度関数≠確率」ではないことに注意して下さい。つまり、IQ110の確率は0.0213ではありません。IQ110の確率を求める場合は次の累積分布関数を使います。
正規分布の累積分布関数ならpnorm関数
Rを使った正規分布の累積分布関数(pnorm)を使えば、正規分布における任意の値以下(以上)の確率を求めることができます。
例えば、先程のIQ110の求め方は、
pnorm(110, mean = 100, sd = 14)
[1] 0.7624747
となり、76.2%がIQ110以下となることが分かります。
もし、IQ110以上の確率を求めたい場合は、pnormのデフォルト設定は"lower.tail = TRUE "となっており任意の値以下の確立が求められるようになっています。そこで、"lower.tail = FALSE"を追加するだけで、任意の値以上の確率が求められます。
pnorm(110, mean = 100, sd = 15, lower.tail = FALSE)
[1] 0.2524925
となり、25.2%がIQ110以上となることが分かります。
でも、まだ何だか数字だけではイメージが沸かないですよね。そこで、tigerstatsパッケージにあるpnormGC関数を使って、累積分布関数を計算してみます。
※tigerstatsを使ったことが無い場合は、install.packages("tigerstats")で先にインストールして下さい。
すると、以下のような結果とグラフが表されます。
library(tigerstats)
pnormGC(110, region = "below", mean = 100, sd = 15, graph = TRUE)
[1] 0.7475075
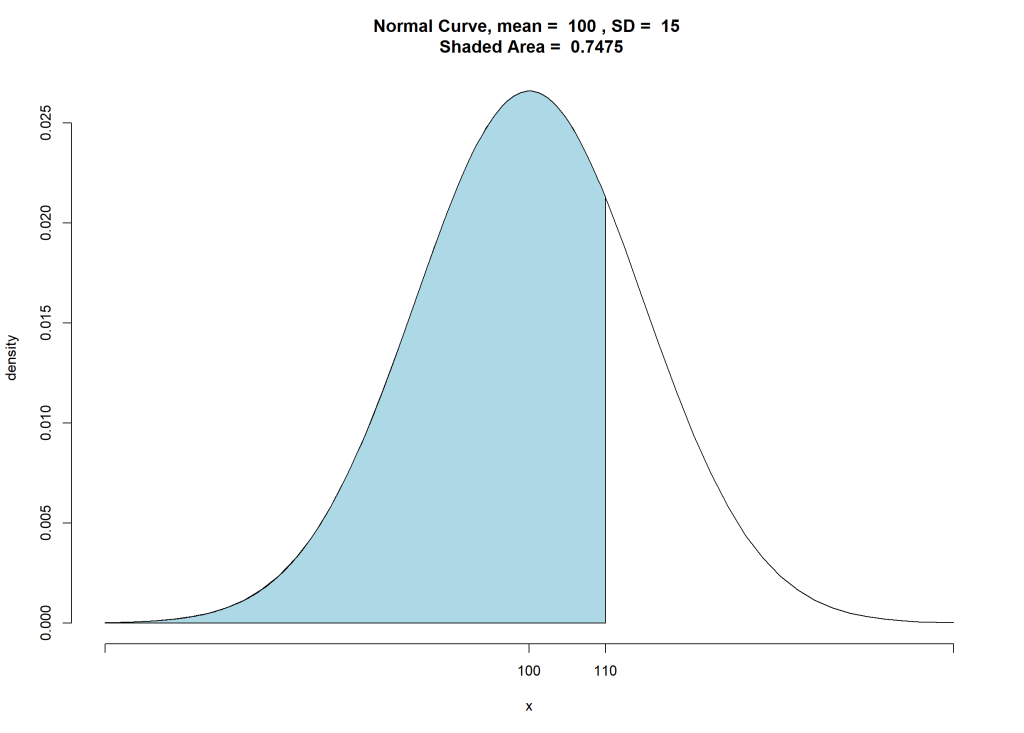
これならグラフで視覚的に捉えられますね。
ちなみに2つの値の間を求めることも簡単ですよ。2つの値と、region = "between"に変更するだけです。
pnormGC(c(85, 115), region = "between", mean = 100, sd = 15, graph = TRUE)
[1] 0.6826895
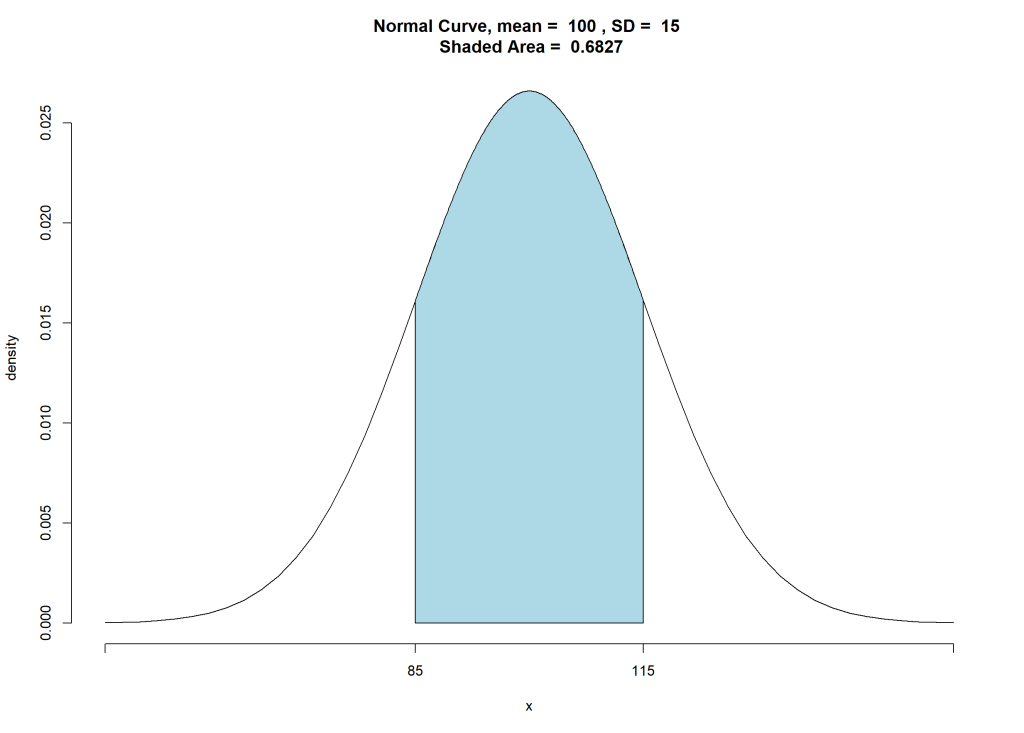
さらに、任意の値以上を見たければ、region = "above"とすればOKです。
パーセンタイル値ならqnorm関数
pnorm関数と逆の関数がqnorm関数です。つまり、正規分布の確率を使ってパーセンタイル値を求めることができます。
例えば、上記で使ったIQの0.7475075となるパーセンタイル値を求める場合、
qnorm(0.7475075, mean = 100, sd = 15)
[1] 110
と、確率を入れれば、110が求められましたね。
さらに、pnomrGCのように視覚的にグラフで表す関数として、qnormGC関数がtigerstatsパッケージには含まれています。
qnormGC(0.7475075, region = "below", mean = 100, sd = 15, graph = TRUE)
[1] 110
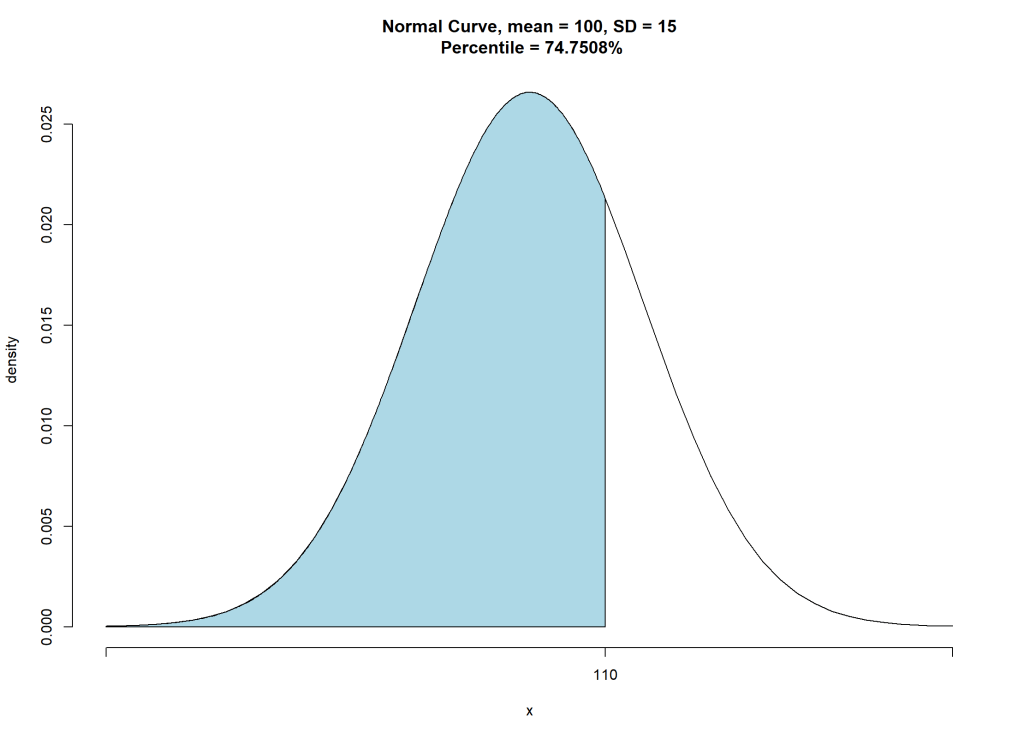
パーセンタイル値を扱う場合は第1四分位数、中央値、第3四分位数など知りたい場合も多いですね。
その場合も、
qnorm(c(.25, .50, .75), mean = 100, sd = 15)
[1] 89.88265 100.00000 110.11735
とすれば大丈夫ですね。
正規分布からランダムな値を求めるならrnorm関数
最後に、rnorm関数ですが、この関数は正規分布からランダムに値を求める場合に使用します。
例えば、
rnorm(3, mean = 100, sd = 15)
[1] 96.25665 94.43266 81.75991
といった感じです。rnorm関数を試してみてください。ランダムだから、上の例とは全く異なる値が得られますよ。
まとめ
正規分布の基本とRを使ったdnorm関数、pnorm関数、qnorm関数、rnorm関数の計算について分かりやすく解説してみました。



コメント