データを収集したら、まずはデータを視覚的に整理する必要があります。その際、度数分布表はとても役立つ整理方法の一つですね。でも、度数分布表って「どうやって作るの?」「データは適当に区切って作るの?」「もしくは作り方のガイドライン的なものはあるの?」といった疑問があると思います。そこで、5STEPで簡単に度数分布表を作る手順とRをちょっと応用してRでの度数分布表の作り方を紹介します。
度数分布表とは
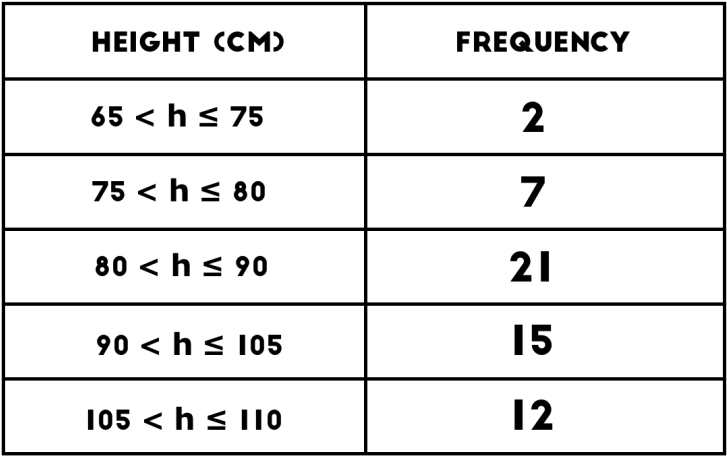
度数分布表とは集めたデータの頻度ーつまり事象発生する回数ーの項目と発生回数を示した表です。例えば以下のようなもの。この場合はある集団の身長を10㎝ずつ区切って、その人数(頻度)をまとめた度数分布表ですね。
度数分布表を作成する5STEPs
まずは手動で作成する5STEPを紹介します。この方法で1度、試しておけば度数分布表の理解が深まります。後述するRを使った方法を行うときも、何となくできたでなく、しっかり理解して作成するためにも是非、試してみてください
5STEPs
- 最大値と最小値を見つけて範囲=最大値ー最小値を求める
- データの中から最大・最小値を見つけます。
- Rならmax(データ名)、min(データ名)、もしくはrange(データ名)で求めることができます。
- 範囲は引き算して下さい。
- 階級の数を決める
- 階級の数の違いでデータはガラっと変わります。研究や調査の目的に沿って階級数を検討しましょう。
- 代表的な方法としてスタージェスの公式:階級の数≒1+3.32log10(データ数)があります。
- 階級間隔を決める
- 安易に間隔を「10刻み」とせずに、STEP1と2で求めた範囲÷階級の数=階級間隔を求めます。
- 求めた階級間隔を基準として、研究・調査の目的なども考慮しながら、「切りの良い」等間隔を選択しましょう。
- 階級境界値と階級値を決める
- 階級間隔が決まったら、階級値と階級上限・下限(以上~未満など)を決めます。
- 度数を数える
- データの度数を数えて表を作成します。
以上が度数分布表を作成する5STEPsです。では実際に具体例を使って説明します。
具体例
例えば、あるシニアクラブのメンバー50人の年齢が、
76,75,83,77,75,76,76,80,90,74,75,80,79,84,79,76,70,78,84,79,73,70,72,74,73,69,74,76,70,82,86,67,80,78,73,69,82,77,76,76,90,76,83,75,76,73,76,69,74,70
だったとします。
度数分布表を作成するならば、
- 最大値:90、最小値:67、範囲:23ですね。
- 階級の数≒1+3.32log10(50)=6.64≒7とします。
- 23÷7=3.28歳となります。年齢ですので、5歳間隔を選択することにします。
- 階級境界値は65歳以上~70歳未満、70歳以上~75歳未満・・・90歳以上~95歳未満とする
- 度数を数える
以上の5STEPsで以下の度数分布表ができました!この程度のデータ数なら手動でも簡単に作成できますね。
| 階級 | 階級値 | 度数 |
| 65歳以上~70歳未満 | 67.5 | 4 |
| 70~75 | 72.5 | 13 |
| 75~80 | 78.5 | 21 |
| 80~85 | 82.5 | 9 |
| 85~90 | 87.5 | 1 |
| 90~95 | 92.5 | 2 |
| 計 | 50 |
Rを応用して度数分布表を作成
Rを使って度数分布表を作成する方法を紹介します。
今回はhist()関数を応用する方法です。このhist()関数はヒストグラムを作図する関数なのですが、ちょっと応用して、引数に、
plot = FALSE
を入れると、グラフではなくヒストグラムに関するデータを表示することができます。
試しに、上のシニアクラブの年齢を使ってみます。まず、年齢をageに代入します。
age <- c(76,75,83,77,75,76,76,80,90,74,75,80,79,84,79,76,70,78,84,79,73,70,72,74,73,69,74,76,70,82,86,67,80,78,73,69,82,77,76,76,90,76,83,75,76,73,76,69,74,70)
そして、hist()関数+plot = FALSEで
hist(age, plot = FALSE)
とすると、RのConsole Paneには以下の結果が表示されます。
$breaks
[1] 65 70 75 80 85 90
$counts
[1] 8 13 20 6 3
$density
[1] 0.032 0.052 0.080 0.024 0.012
$mids
[1] 67.5 72.5 77.5 82.5 87.5
$xname
[1] "age"
$equidist
[1] TRUE
attr(,"class")
[1] "histogram"
ここで、黄色でハイライトした部分に注目してください。
・ $breaksは階級間隔
・ $countsが度数
・ $midsが階級値
なのですが、手で計算したのと、度数が異なることに気づきましたか?
実は、hist()のデフォルトでは$breakは65<x≦70となっているのです。
さらにデフォルトではRが気を利かせて自動で階級を分けてくれているのですが、この時、Rはさらに気を利かせて最小値や最大値をまとめてしまうことがあります。
この対策方法として、
まず、引数に
- right = FALSE ←以上~未満に変更
- breaks = seq(階級の最小値, 階級の最大値, 間隔) ←最小値や最大値がまとめられないようにする
を代入します。例を使えば、こんな風です。
age_hist <-hist(age, plot = FALSE, right = FALSE, breaks = seq(65, 95, 5))
こうすれば、
$breaks
[1] 65 70 75 80 85 90 95
$counts
[1] 4 13 21 9 1 2
$density
[1] 0.016 0.052 0.084 0.036 0.004 0.008
$mids
[1] 67.5 72.5 77.5 82.5 87.5 92.5
$xname
[1] "age"
$equidist
[1] TRUE
attr(,"class")
[1] "histogram"
となりました。
説明すると長々となりましたが、応用するポイントは2つなので、慣れれば簡単です。
では、度数分布表を作成しましょう。
範囲の列名を作成します。
range <-c("65-70","70-75","75-80","80-85","85-90","90-95")
では、data.frame()関数を使って、度数分布表を作ります。
freq.table <- data.frame(range, mids = age_hist$mids, frequency = age_hist$counts)
freq.table
range mids frequency
1 65-70 67.5 4
2 70-75 72.5 13
3 75-80 77.5 21
4 80-85 82.5 9
5 85-90 87.5 1
6 90-95 92.5 2
まとめ
度数分布表の作り方はとても簡単です。ヒストグラム同様に記述統計の基本となります。データの傾向や特徴を掴むのにも役立ちますので、是非、試してみてください。


コメント