はじめに
データのパターンや関連性を理解するために統計分析を使うことは多いと思います。最も頻繁に利用されるのは2群間での平均の差の検定だと思いますが、いつも2群間での比較検討ばかりではありませんよね。時には3群以上の比較検討が必要な場合もあると思います。そんな時、力を発揮してくれるのが、一元配置分散分析(ANOVA)です。一次元配置分散分析(ANOVA)は、異なるグループ間の平均値比較を分散を使うことによって、統計的な有意差を検出するための手法です。
本記事では、PythonのパッケージであるStatsmodelsを使って、一次元配置分散分析を行う方法について解説します。さらに、初心者でも理解しやすいように、具体的なコード例を交えながら説明していきます。
一元配置分散分析(ANOVA)の基本
一元配置分散分析は、1つの説明変数に対して、複数のグループ(群)間での平均値に統計的な差があるかどうかを検定します。具体的な例を通じて、一元配置分散分析の基本的な概念を説明します。

例えば、ある薬の効果を検証するために、3つのグループに対してそれぞれ異なる薬を投与し、その効果を測定したいとします。3つのグループは、「薬A」、「薬B」、「薬C」としましょう。(※各グループ被験者数が異なっていても構いません。)
仮説:
- 帰無仮説(H0): グループの平均値に統計的な差はない。
- 対立仮説(H1): 少なくとも1つのグループの平均値は他のグループと統計的に異なる。
となりますね。
一元配置分散分析の詳しい解説については下記のLINKを参照にしてください。
PythonのStatsmodelsを使って簡単に一元配置分散分析を求める
では、統計学的な分散分析の説明は脇に置いておいて、早速Statsmodelsを使ってANOVAを求めていきましょう。
Statsmodelsのインストール:
まず最初に、Statsmodelsパッケージをインストールする必要があります。以下のコマンドを使用して、簡単にインストールすることができます。
pip install statsmodelsもし、Jupyter Notebook上でライブラリーをインストールする場合は下のように「!pip」とpipの前に「!」を追加して「Shift + Enter」すればOKです。
!pip install statsmodelsサンプルデータの準備:
データの準備:
一次元配置の分散分析を行うためには、それぞれのグループに属するサンプルの値を含む配列データを準備する必要があります。また、各グループのサンプル数は同じである必要はありません。
例えば、ほぼ同じ学力レベルに振り分けられた中学1年生3クラスがあり、以下の表のような数学テスト結果が得られたとします。それぞれの異なる数学教師が授業を受け持っている場合、これらの3クラスの成績と教師の指導方法に差があるのでしょうか?
| class_A | class_B | class_C |
| 95 | 83 | 68 |
| 91 | 89 | 75 |
| 89 | 85 | 79 |
| 90 | 89 | 74 |
| 99 | 81 | 75 |
| 88 | 89 | 81 |
| 96 | 90 | 73 |
| 98 | 82 | 77 |
| 95 | 84 | 80 |
上のサンプルデータをpythonコードで書くと、
import numpy as np
import pandas as pd
class_A = np.array([95, 91, 89, 90, 99, 88, 96, 98, 95])
class_B = np.array([83, 89, 85, 89, 81, 89, 90, 82, 84])
class_C = np.array([68, 75, 79, 74, 75, 81, 73, 77, 80])
# データを結合する
data = np.concatenate([class_A, class_B, class_C])
# グループのラベルを作成
labels = ['class_A'] * len(class_A) + ['class_B'] * len(class_B) + ['class_C'] * len(class_C)
# データとラベルからデータフレームを作成
df = pd.DataFrame({'data': data, 'group': labels})いきなり分散分析に進むのではなく、データを視覚的に確認しましょう
import seaborn as sns
sns.boxplot(x="group", y="data", data=df)上のコードを実行すると箱ひげ図が作成されます。
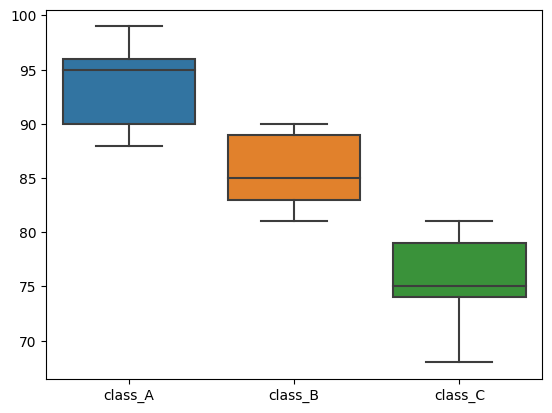
う~ん。見るからに各クラスの数学の点数には差があり、指導方法が影響している可能性がありそうですね。
Statsmodelsを使った一次元配置の分散分析の実行:
それでは、Statsmodelsを使って一次元配置の分散分析を実行してみましょう。
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# 一次元配置の分散分析モデルを作成
model = ols('data ~ group', data=df).fit()
# 分散分析結果を取得
anova_result = anova_lm(model)
# 結果を表示
print(anova_result)上記のコードを解説します。
ols関数
まず、ols関数を使用して一次元配置の分散分析モデルを作成し、fitメソッドを呼び出してモデルをフィットさせます。
ols関数は、Statsmodelsパッケージの中のformula.apiモジュールから提供される関数です。一元配置の分散分析モデルを作成するためには、ols関数に対して2つの引数を渡す必要があります。
- 第1引数:分析対象のデータを表す数式の形式で指定します。ここでは、"data ~ group"という数式を指定します。"data"は従属変数(説明したい現象)を示し、"group"は独立変数(グループ)を示します。
- 第2引数:分析対象のデータを保持しているデータフレームを指定します。このデータフレームには、従属変数と独立変数のデータが含まれています。
ols関数の後に作成したモデルをフィットさせるために、fitメソッドを呼び出します。fitメソッドは、モデルを実際のデータに適合させるためのメソッドです。この適合の過程によって、モデルのパラメータが推定されます。
anova_lm関数
次にanova_lm関数を使って分散分析結果を取得します。
anova_lm関数は、Statsmodelsパッケージの中のstats.anovaモジュールから提供される関数です。この関数は、一元配置分散分析の結果を取得するために使用されます。
結果の見方
最後にprint関数を使って結果を表示しています。結果は以下のようになります。
df sum_sq mean_sq F PR(>F)
group 2.0 1412.666667 706.333333 47.440299 4.583563e-09
Residual 24.0 357.333333 14.888889 NaN NaN分散分析の結果には、グループ間の差異に基づくF値やp値などが含まれます。ここで、
df:自由度sum_sq:平方和mean_sq:平均平方F:F値PR(>F):p値
を表します。もしp値が有意水準(通常は0.05)よりも小さい場合、グループ間に統計的に有意な差があると結論付けることができます。
今回の結果、p値<0.05ですから、「帰無仮説(H0): 各クラスの平均値に統計的な差はない」は棄却され、対立仮説(H1)である「少なくとも1つのクラスの平均値は他のグループと統計的に異なる」ということが結論付けられます
まとめ:

本記事では、PythonのStatsmodelsパッケージを使用して一次元配置の分散分析を行う方法について解説しました。Statsmodelsを使うことで、統計的な有意差を検出するための一次元配置の分散分析を簡単に実行することができます。初心者の方でも分かりやすいように、具体的なコード例を交えて手順を説明しました。是非、自分のデータに適用してみてくださいね。





コメント