時系列データとは?
時系列データとは、時間の流れに沿って観測されたデータのことを指します。言い換えれば時間軸を持ったデータです。
例えば、
- 毎年の出生数
- 月ごとの売上
- 毎日の気温
など、時間とセットになっているデータのことを指します。こうしたデータには「時間軸」が存在しており、それが他の変数と異なる特徴になります。
図にするとこんな感じ👇
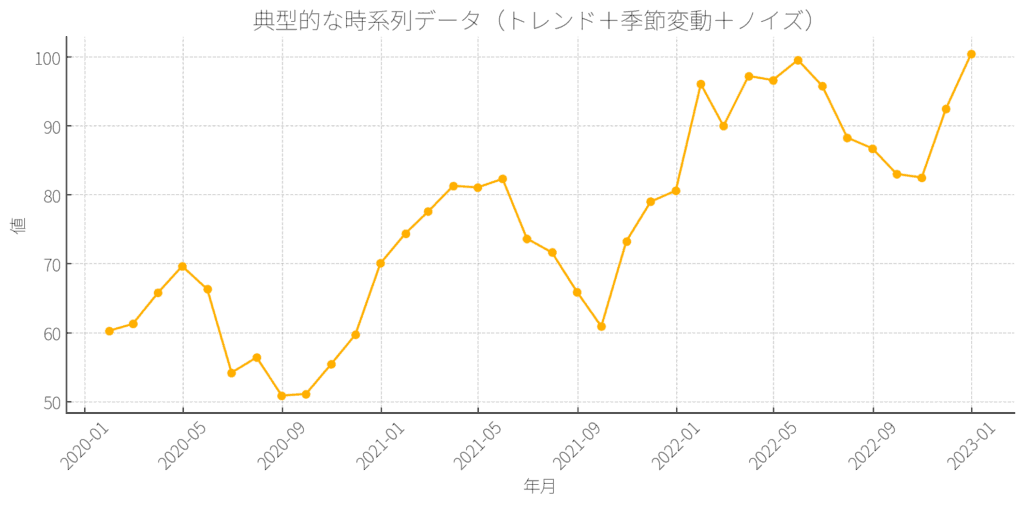
- 横軸:時間(年や月など)
- 縦軸:観測された数値
このように、横軸に時間をとり、縦軸に数値を示すことで、時間とともにどのように変化しているかが視覚的にわかります。
データの変化を見る方法
時系列データでは、「時間とともにどう変わったか?」が大事なポイントです。
その変化の見方にはいくつかの方法があります。
① 差(変化量)
時系列データを記述するための方法はいくつかあります。まず基本となるのは、「差」を見る方法です。ある時点とその次の時点の差を見て、どれくらい変わったかを調べます。
ここで t はある時点を表しており、t+1 はその次の時点です。それぞれの時点におけるデータを比較することで、どれだけ変化したかを把握することができます。
公式:
$$ 差分=Y_{t+1}−Y_t $$
これは、時点 t から t+1 への絶対的な変化量を表します。
例:
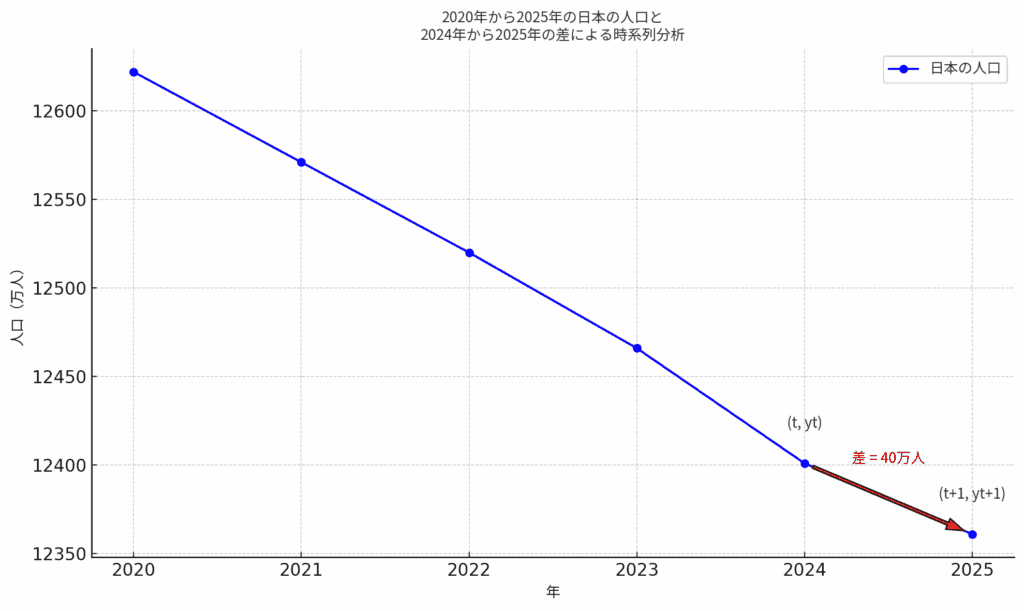
たとえば、2024年の人口をある基準点として、その次の2025年のデータと比べて変化の大きさを見るといった具合です。差の計算はシンプルで、t+1の値からtの値を引くだけです。
2024年の人口が12400万人、2025年が12360万人だったら、
12400−12360=−40(万人)
つまり、40万人減ったということですね。
➁ 変化率(何%増えた?減った?)
今度は、「元の値に比べてどれくらい変化したのか?」を見ます。これは、単なる差ではなく、変化量を元の値で割って計算します。どのくらいの割合で増減したのかを把握するのに役立ちます。
これが 変化率です。
公式:
$$変化率 = \frac{Y_{t+1} - Y_t}{Y_t} $$
変化率を用いることで、元の値の大きさに関係なく、変動の割合を比較することが可能です。
先ほどの人口変化を変化率で表現すると以下のようになります。
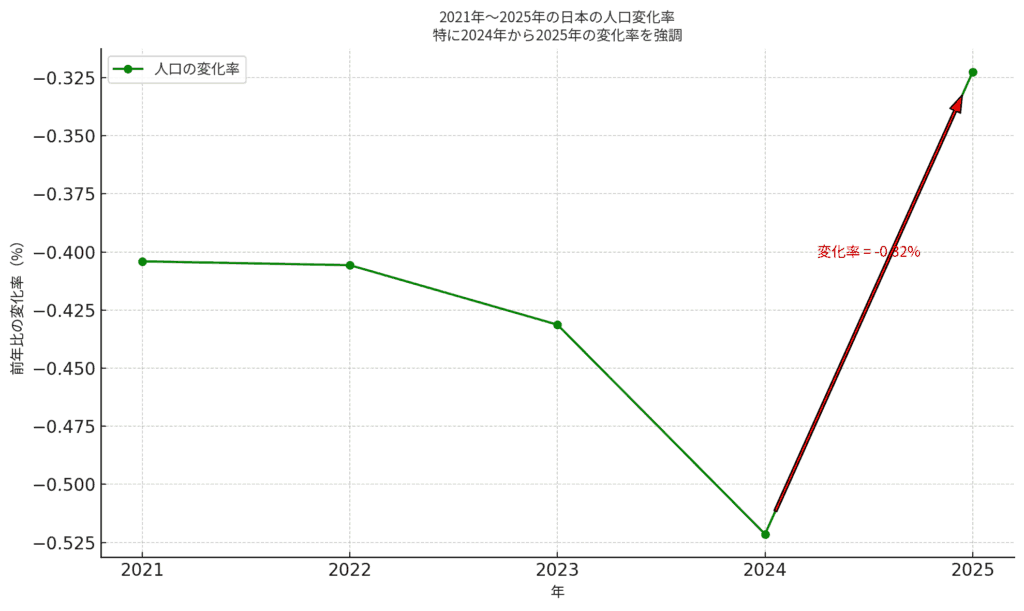
上のグラフは、「人口の減り方がどのくらいか」を % で教えてくれています。ここから、毎年人口が少しずつ減っていることがわかりますね。
また、「変化率」を見ることで、「ただ減っている」だけじゃなく「どれくらいの速さで減っているか」もわかります。
上図の矢印と赤文字は、2024年から2025年の変化に注目しています。このときの変化率は「−0.32%」ですから、前の年(2024年)と比べて、人口が0.32%減った、ということです。また、「2022年や2023年に比べると、減るスピードは少しゆるやかになっている」ことがわかりますね。
例:
変化率を使う一般例として、ビジネスでの売り上げがあります。
例えば、売上が 100万円 → 120万円 に増えたら、
$$\frac{120 - 100}{100} \times 100\% = 20\%$$
つまり、20%アップです!
③ 平均的にどれくらい増えてる?(幾何平均)
長い期間の変化を「1年あたりで平均するとどれくらい?」と知りたいときは、幾何平均(きかへいきん)という方法を使います。
たとえば、ある値が5年で100から120に増えた場合、単純に「増えた20」を5で割って4%の年平均増加とはできません。
実際には、「5年間で100から120(1.2倍)になった」ことから、変化率を5乗して120(1.2倍)になるような年平均の変化率を計算する必要があります。
このときの計算は、1.2の5分の1乗を求めることで得られます。
公式:
$$1 + r = \left( \frac{Y_t}{Y_0} \right)^{1/t}$$
このように、幾何平均成長率は「累積変化を年平均に平準化」した指標です。
例:
100が5年後に120になった場合:
$$1 + r = \left( \frac{120}{100} \right)^{1/5} \approx 1.0371
→ r ≒ 3.71\%$$
つまり、毎年平均して約3.7%ずつ増えているということになります。
④ 指数化(基準を「100」にする)
さらに、データを「指数化」する方法もあります。これは、ある時点の値を基準として「100」とし、それ以外の時点の値が基準に対してどれくらいの水準かを相対的に表す方法です。基準時点の値を物差しの1目盛りとしたとき、他の時点の値が何目盛り分になるかを示すイメージです。
指数化することで基準時点をベースにしながら複数の異なる時点の比較がしやすくなります。
公式:
$$指数 = \frac{Y_t}{Y_{\text{基準}}} \times 100$$
例:
2000年を100としたとき、2005年の値が120なら:
$$\frac{120}{100} \times 100 = 120$$
なので、「2005年は2000年に比べて20%増」ということが一目でわかります。
ラスパイレス指数ってなに?
ちょっと専門的な話ですが、「ラスパイレス(価格)指数」という有名な指数もあります。これは複数の品目の価格と数量をもとに算出される指数で、基準時点の価格と数量を用いて「重み」を作成し、その重みに基づいて比較時点の変化を評価します。
ラスパイレス指数の便利な点は、重みを頻繁に更新しなくてもよいところにあります。
公式 (2品目の場合):
$$\frac{\sum_{i=1}^{2} w_i \left( \frac{p_{ti}}{p_{0i}} \right)}{\sum_{i=1}^{2} w_i} = \frac{w_1 \left( \frac{p_{t1}}{p_{01}} \right)}{w_1 + w_2} + \frac{w_2 \left( \frac{p_{t2}}{p_{02}} \right)}{w_1 + w_2} = \frac{p_{t1} q_{01} + p_{t2} q_{02}}{p_{01} q_{01} + p_{02} q_{02}}$$
説明:
- \(p_{0i}\):基準時点の第\(i\)品目の価格
- \(q_{0i}\):基準時点の第\(i\)品目の数量
- \(p_{ti}\):比較時点の第\(i\)品目の価格
- \(q_{ti}\):比較時点の第\(i\)品目の数量
- \(w_i = p_{0i} q_{0i}\):ウェイト(基準時点の価格と基準時点の数量の積により計算)
- \(\frac{p_{ti}}{p_{0i}}\):第\(i\)品目の基準時点に対する比較時点の価格指数
式だけ見ると難しそうですが、要点としては、基準時点の価格と数量を使って重みづけし、その重みを用いて比較時点の価格を評価するというものです。
例題:2つの商品でラスパイレス指数を計算してみよう!
| 品目 | 基準時の価格 (\(p_{0i}\)) | 基準時の数量 (\(q_{0i}\)) | 比較時の価格( \(p_{ti}\)) |
|---|---|---|---|
| A(米) | 100円 | 10袋 | 120円 |
| B(卵) | 200円 | 5パック | 180円 |
▼ ステップ1:ウェイト(重み)を計算
$$w_1 = p_{01} \times q_{01} = 100 × 10 = 1000$$
$$w_2 = p_{02} \times q_{02} = 200 × 5 = 1000$$
▼ ステップ2:各品目の価格変化率を計算
米の価格変化: $$\frac{120}{100} = 1.20$$
(20%アップ)
卵の価格変化: $$\frac{180}{200} = 0.90$$
(10%ダウン)
▼ ステップ3:ラスパイレス指数を計算
$$\frac{w_1 \cdot \frac{p_{t1}}{p_{01}} + w_2 \cdot \frac{p_{t2}}{p_{02}}}{w_1 + w_2} = \frac{1000 × 1.20 + 1000 × 0.90}{1000 + 1000} = \frac{1200 + 900}{2000} = \frac{2100}{2000} = 1.05$$
▼ 結果:ラスパイレス指数 = 1.05
これは「全体として物価は5%上がった」という意味です。
時系列データの中身を分解してみよう
時系列データは、いろんな変化が混ざっています。
この時系列データを、3つの成分に分けて考えます:
Yt = 傾向変動(TC)+季節変動(S)+不規則変動(I)
時系列データは、単に時間順に並んだ数値ではなく、「時間によって変化する」という点に大きな意味があります。そのため、データの変動がどのような要因で生じているのかを分析することが重要です。
時系列データは、次のような形で分解することができます:
$$Y_t=TC_t+S_t+I_t$$
ここで、
- \(Y_t\):ある時点 tの観測値
- \(TC_t\):傾向変動(Trend & Cycle)
- \(S_t\):季節変動(Seasonal Variation)
- \(I_t\):不規則変動(Irregular Variation)
① 傾向変動(Trend / Cycle)
時間が経つにつれてじわじわ変わっていくもの。たとえば:
- 少子化で出生数がだんだん減っていく
- 技術革新で生産量が増えていく
こんな長期的な流れを「傾向変動」といいます。
景気のように3~15年くらいで上がったり下がったりするものは「循環変動(サイクル)」とも呼ばれます。
② 季節変動(Seasonal)
1年の中で繰り返すパターン。たとえば:
- 夏にエアコンの電気代が上がる
- 冬におでんの売上が増える
こういう、毎年決まって現れる波が「季節変動」です。
③ 不規則変動(Irregular)
予想できない、突発的な変動のことです。
- 台風でお店が休業
- コロナ禍の影響で売上激減
など、時間の流れとは関係ない“例外的”な変化です。
自己相関ってなに?
自己相関とは、「過去の自分のデータと今のデータが似てるかどうか」を調べることで、言い換えれば「ある時点のデータと、過去のデータ(遅れ=ラグ)との関係の強さ」を示すものです。
「ラグ1」なら「1か月前」など、直前の時点との関係を見ているという意味です。
- 「ラグ1」は「1つ前のデータ」との関係
- 「ラグ2」は「2つ前のデータ」との関係
- …というふうに、どのくらい過去のデータが現在のデータに影響しているかを数値で表します。
たとえば、売上が「毎月なんとなく似た動き」をしているなら、自己相関が高いといえます。
🔹 自己相関係数の値の意味
- +1 に近い(例:0.642) ⇒ 強い「正の相関」:過去が高ければ現在も高い傾向
- 0 に近い(例:-0.018) ⇒ ほとんど相関がない
- 1 に近い(例:-0.610) ⇒ 強い「負の相関」:過去が高ければ現在は低い傾向(反対の動き)
例えば、
| ラグ(遅れ) | 自己相関係数 |
|---|---|
| 1 | 0.642 |
| 2 | -0.018 |
| 3 | -0.317 |
| 4 | -0.329 |
| 5 | -0.610 |
- ラグ1(1つ前)で相関係数が0.642 → 1時点前の値と今の値には強い関係がある。 → たとえば「今月の売上は、先月と似ている」傾向があるといえる。
- ラグ2以降は相関が小さい・マイナス → 2か月前以降の影響はほとんどない、または逆の動きをしている。
自己共分散の式
この自己相関係数を計算するために必要なのが、「自己共分散(じこきょうぶんさん)」というものです。
「自己共分散」は、自分自身のデータを少し時間をずらして(=タイムラグをとって)比べることで求めます。
たとえば、「1か月前(ラグ1)」のデータと「今月」のデータがどのように動いているかを比べてみます。
まずは「どれくらい一緒に動いてるか?」を調べる「自己共分散」を計算します。
自己共分散は、次のように計算されます:
- 各月のデータから「平均」を引いて、どのくらいズレているかを計算します。
- そのズレを、「今月」と「ラグをずらした月」との間で掛け合わせていきます。
- それを合計し、観測期間に合わせて調整します。
これを公式に書くと:
$$\gamma_k = \frac{1}{N} \sum_{t=1}^{N-k} (Y_t - \mu)(Y_{t+k} - \mu)$$
ここで:
- \(\gamma_k\):タイムラグkにおける自己共分散
- \(Y_t\):時点tのデータ
- \(\mu\):平均(全データの平均値)
- \(N\):データの全件数
- \(k\):タイムラグ(何期前と比べるか)
上の公式はかなり難しく感じますね。この公式をさらに読み替えていきます。
1️⃣ \(Y_t - \mu\):
今の値 \(Y_t\)が、平均からどれくらい離れているか(偏差)。
2️⃣ \(Y_{t+k} - \mu\):
k 期先の値が、平均からどれくらい離れているか。
3️⃣ その積:
今と k 期先が「同じ方向にずれていれば正」「逆方向なら負」になる。
4️⃣ 全部のデータで足し算して平均:
データ全体でその傾向を見ている。
そもそも「共分散」って?
共分散は「2つの変数がどれくらい一緒に動いているか」を測る指標です。
- 大きいとき → 一緒に増減しやすい
- 小さい(負のとき) → 逆の動きをしやすい
自己共分散はこれを「自分自身のデータ同士」で計算したものです。
具体的には「今の値と k 期前の値の一緒の動き」を見ます。
例えば次のようなデータがあったとします:
| 時点(t) | \(Y_t\) |
|---|---|
| 1 | 100 |
| 2 | 110 |
| 3 | 105 |
| 4 | 115 |
| 5 | 120 |
平均は \(\mu = 110\)。
タイムラグ \(k=1\) のとき:
- (1期目と2期目) の偏差の積:
(100−110)×(110−110)=(−10)×0=0 - (2期目と3期目) の偏差の積:
(110−110)×(105−110)=0×(−5)=0 - (3期目と4期目) の偏差の積:
(−5)×5=−25 - (4期目と5期目) の偏差の積:
5×10=50
これらを合計して平均を取れば、「1期遅れの自己共分散」になります。
自己共分散は、過去のデータとどれくらい一緒に動いたかを確認するための指標です。
一見すると公式は難しそうに見えますが、実際の流れはシンプルで、
「各時点のデータと平均の差(偏差)を計算し、それらの積を足し合わせて平均を取る」
という手順です。
また、特に重要なポイントとして、タイムラグが0のときは、自己共分散は通常の分散と同じ意味になることも覚えておくと理解が深まります。
自己共分散の意味と解釈
自己共分散を理解するうえで、「ラグ(遅れ)」の考え方が重要ですので、もう一度おさらいします。
ラグとは、どれくらい前のデータと今のデータを比べているか、という時間のずれを意味します。たとえば「ラグ1」というのは、1つ前の時点、つまり1か月前や1日前などのデータと比べていることを指します。「ラグ2」であれば2か月前、2日前といったように、比較の基準となる時間がさらに前になります。
このラグを使って求められる自己共分散は、たとえば「ラグ1の自己共分散」であれば、
「今のデータと1か月前のデータのばらつき具合がどのくらい似ているか、
そしてどれくらい一緒に動いているか」
を数値として表しています。
では、自己共分散の値が大きいというのは、どういう意味を持つのでしょうか。
たとえば、「ラグ1の自己共分散が大きい」というのは、今月と1か月前のデータが、平均からのズレ方までよく似ていて、しかもその動きが同じ方向にそろっていることを意味します。言い換えれば、「先月の値が平均より高いとき、今月の値も高くなりやすい」といった傾向があるということです。
このように、自己共分散は「過去の自分と今の自分がどれくらい同じように動いているか」を見つけるための、大切な道具になります。特に時系列データを扱うときには、「データの中に時間的なつながりがあるか?」を判断するための出発点として、とても重要な役割を果たします。
自己相関係数の式
自己共分散を「分散」で割って標準化すると、「自己相関係数」になります。
公式:
$$\rho_k = \frac{\gamma_k}{\gamma_0}$$
値は -1〜+1 の間をとり、
- +1 に近い → 似ている(正の相関)
- 0 に近い → 関係ない
- 1 に近い → 逆の動き(負の相関)
自己共分散の際に示したデータを使って、タイムラグ1(1期遅れ)の自己相関係数を求めてみます。
▼ ステップ1:データの平均を求める
全データの平均(μ):
$$\mu = \frac{100 + 110 + 105 + 115 + 120}{5} = \frac{550}{5} = 110$$
▼ ステップ2:分散(タイムラグ0の自己共分散)を求める
自己相関係数の計算には、分散(自己共分散の基準値)が必要です。
分散は次の式で求めます:
$$\gamma_0 = \frac{1}{N} \sum_{t=1}^N (Y_t - \mu)^2$$
計算すると:
| t | \(Y_t\) | \(Y_t − μ\) | \((Y_t − μ)^2\) |
|---|---|---|---|
| 1 | 100 | -10 | 100 |
| 2 | 110 | 0 | 0 |
| 3 | 105 | -5 | 25 |
| 4 | 115 | 5 | 25 |
| 5 | 120 | 10 | 100 |
合計: 100+0+25+25+100=250
したがって、
$$\gamma_0 = \frac{250}{5} = 50$$
▼ ステップ3:タイムラグ1の自己共分散を求める
タイムラグ1の自己共分散\(γ₁\)は:
$$\gamma_1 = \frac{1}{N} \sum_{t=1}^{N-1} (Y_t - \mu)(Y_{t+1} - \mu)$$
計算の対応:
| ペア | \((Y_t − μ)\) | \((Y_{t+1} − μ)\) | 積 |
|---|---|---|---|
| 1と2 | -10 | 0 | 0 |
| 2と3 | 0 | -5 | 0 |
| 3と4 | -5 | 5 | -25 |
| 4と5 | 5 | 10 | 50 |
合計: 0+0+(−25)+50=250 + 0 + (-25) + 50 = 250+0+(−25)+50=25
したがって:
$$\gamma_1 = \frac{25}{5} = 5$$
▼ ステップ4:自己相関係数を計算
自己相関係数(ρ₁)の公式:
$$\rho_1 = \frac{\gamma_1}{\gamma_0}$$
数値を代入すると:
$$\rho_1 = \frac{5}{50} = 0.1$$
▼ まとめ
- 分散(γ₀)を計算して基準にする
- タイムラグ1の自己共分散(γ₁)を計算する
- ρ₁ = γ₁ / γ₀ で自己相関係数を求める
今回の例では: \(\rho_1 = 0.1\)
→ 「1期前のデータとは弱い正の相関がある」と解釈できます。
コレログラムで「パターン」を見つけよう
「コレログラム」は、自己相関係数のグラフです。
横軸がタイムラグ(何か月前)、縦軸が自己相関係数になっていて、
- 高いところが定期的に出てくると → 周期性がある!
- だんだん下がると → トレンドかも?
…というふうに、データの隠れたリズムを見つけられます。
コレログラムを計算してみましょう
あるお店の 月ごとの売上(単位: 万円)が次の通りだったとします:
| 月 | 売上(万円) |
|---|---|
| 1 | 100 |
| 2 | 120 |
| 3 | 130 |
| 4 | 90 |
| 5 | 80 |
| 6 | 110 |
| 7 | 120 |
| 8 | 130 |
| 9 | 90 |
| 10 | 80 |
| 11 | 110 |
| 12 | 120 |
🔢 自己相関係数を計算する
タイムラグ(遅れ)を 1ヶ月, 2ヶ月, 3ヶ月…と変えて計算。
結果として、以下の表になります:
| タイムラグ(ヶ月) | 自己相関係数(r) |
|---|---|
| 1 | 0.75 |
| 2 | 0.50 |
| 3 | 0.10 |
| 4 | -0.30 |
| 5 | -0.60 |
| 6 | -0.80 |
コレログラム図のイメージ
この表をグラフにすると:
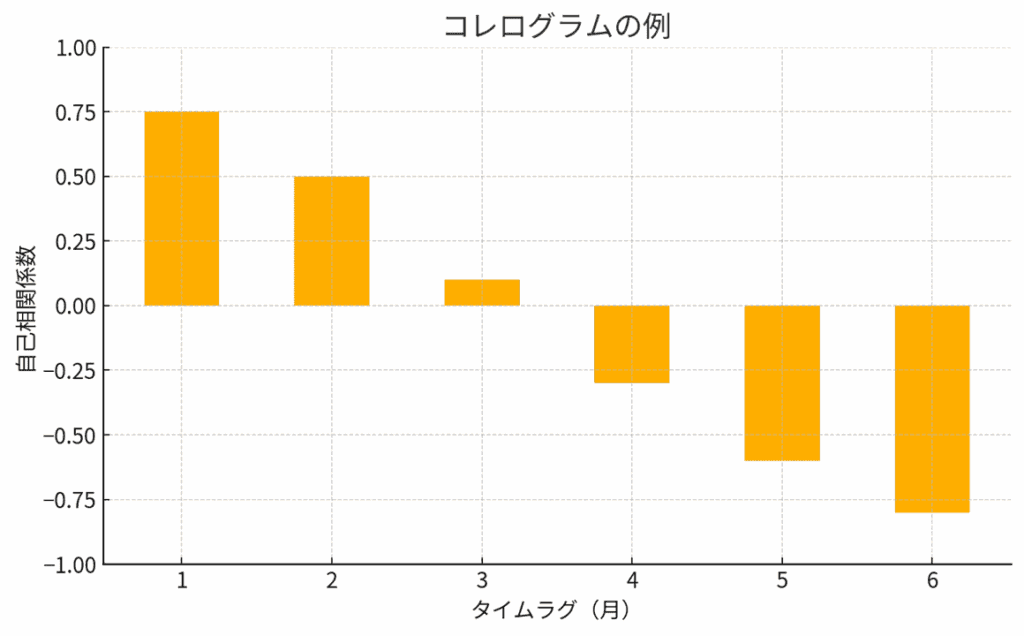
- 横軸:タイムラグ(月)
- 縦軸:自己相関係数(r)
🔔 解釈のポイント:
- Lag1で0.75 → 直近1ヶ月前の売上と強い正の相関あり(よく似てる)
- Lag6で-0.80 → 6ヶ月前と逆の動きになりやすい(負の相関強い)
まとめ

時系列分析は、データの変化を「時間の流れ」という視点から理解するための手法です。分析の基本として、差分や変化率、幾何平均変化率、指数化などの方法があります。さらに、データの「時間による依存関係」を調べるために自己共分散が使われ、これらの自己相関をまとめて視覚化したものがコレログラムです。こうした考え方を身につけることで、時系列データの構造をしっかり捉え、変動の要因を理解できるようになります。
| 方法 | 意味 | 公式・ポイント |
|---|---|---|
| 差分 | どれだけ変わった? | \(Y_{t+1} - Y_t\) |
| 変化率 | 何%変わった? | \(\frac{Y_{t+1} - Y_t}{Y_t} \times 100\%\) |
| 幾何平均 | 平均するとどれくらい? | \(\left(\frac{Y_t}{Y_0}\right)^{1/t}\) |
| 指数化 | 基準を100に揃える | \(\frac{Y_t}{Y_0} \times 100\) |
| 自己相関 | 過去と似てる? | \(\rho_k = \frac{\gamma_k}{\gamma_0}\) |



コメント