この記事では、量的変数の分布に関する特徴を把握するための数値的な指標について学習します。具体的には、「中心の指標」と「散布の指標」がメインテーマです。
平均とは中心の指標

データをたくさん集めたとき、その「だいたいの真ん中」はどこにあるのかを知りたいですよね。
そんなときに使うのが「平均」という数字です。
平均は、すべてのデータを足してから、その数で割ることで求められます。たとえば10人のテストの点数があったら、合計して10で割るという感じです。数式で表すと以下のようになります。
$$\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i$$
ここで、
$$\sum$$は総和を表す記号で、
$$\sum_{i=1}^{n} x_i = (x_1 + x_2 + \ldots + x_n)$$
は各観測値で、1~n個までのデータを足すという意味です。
この平均という値は、「データ全体の重心」みたいな役割をしてくれていて、全体のバランスのとれた場所を表しています。
例えば、以下のような10個のデータがあったとします。
12, 15, 20, 22, 18, 30, 25, 16, 19, 21
平均はすべての値の合計をデータ数で割って求めます。
$$\text{平均} = \frac{12 + 15 + 20 + 22 + 18 + 30 + 25 + 16 + 19 + 21}{10}$$
計算結果は、
平均=19.8
ただし、平均値はすべての観測値の影響を等しく受けるため、外れ値の影響を受けやすい特徴があります。言い換えると、すごく高い値やすごく低い値が混ざっていると、平均はその影響を強く受けてしまいます。だから、データに極端な値(=外れ値)があるときは、中央値など他の指標を用いる方が適切な場合もあります。
分散と標準偏差ってどういう意味?
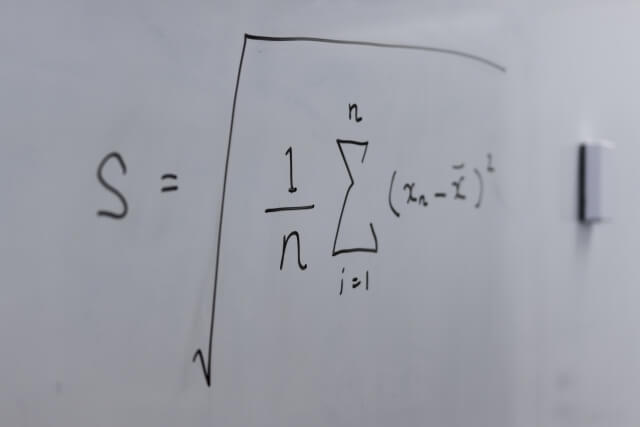
今度は分布の「ばらつき(散らばり具合)」を見てみましょう。
たとえば、全員が似たような点数だったのか、それとも高い人も低い人もいてバラバラだったのか、すなわち観測値が中心からどの程度離れているかを示す代表的な指標が分散と標準偏差です。
まず、「分散」は、平均からどれだけ離れているかを2乗して、すべて足し合わせて、データの数で割って求めます。
分散は以下の式で定義されます。
$$s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2$$
つまり分散は各観測値と平均値の差(偏差)を2乗し、それを平均したものです。偏差を2乗することで、正負の差が打ち消し合うのを防ぐとともに、大きく離れた値の影響を強調することができます。
でも、分散はちょっと難しいのが、元の単位と違う単位(平方)になってしまうこと…。例えばクラスの身長(cm)の分散を計算すると、平方センチメートルになります。
$$ cm^2 $$
そこで出てくるのが標準偏差です。
$$s = \sqrt{s^2}$$
標準偏差は、分散の平方根(ルート)をとって、元の単位に戻したものでばらつきを示す指標として広く用いられます。上の例なら、
$$\sqrt{cm^2} = cm$$
そして分散の値が大きいと「データのばらつきが大きい」、小さいと「データがまとまっている」と考えます。
標準化得点(z得点)ってなに?

異なる変数間での比較を可能にするための指標として、標準化得点(z得点)があります。たとえば、英語と数学のテストで平均点が違う場合、「どっちが良い点だったのか」を比べるのって難しいですよね。
そんなときに便利なのが標準化得点(z得点)です。
これは、
$$z = \frac{x - \bar{x}}{s}$$
「自分の点数 − 平均点」 ÷ 標準偏差
という計算で求められます。
この指標は、観測値が平均からどれほど離れているかを、標準偏差を単位として表したものです。標準化により、どんなデータでも「平均が0、ばらつきが1」という共通ルールに変えることができ、異なる変数間での比較が可能となります。
つまり、違う種類のデータでも公平に比べられるようにするための工夫なんですね。
変動係数ってどんなもの?
変数間でばらつきの大小を比較するためのもう一つの指標が変動係数です。これは、標準偏差を平均で割ったものです。
これは以下の式で定義されます。
$$CV = \frac{s}{\bar{x}}$$
標準偏差を平均値で割ることにより、相対的なばらつきを示すことができます。値の単位やスケールが異なる変数間においても、比較が容易となる点で有用な指標です。
たとえば、身長と体重のばらつきを比べたいとき、単位も大きさも違うので、単純に標準偏差だけを見ても比べにくいですよね。
そこで、平均を「ものさし」にして「平均に対してどれくらいばらついているか」を見るのが変動係数です。
このように、変動係数は、別々の単位のデータどうしのばらつきを比べたいときに使える便利な指標なんです。
標準化得点?変動係数?どっち?
ここで「標準化得点と変動係数は何が違うの?」という疑問が生じませんか?
標準化得点(z得点)と変動係数(CV)は、どちらも異なる単位やスケールのデータを比較するときに使える指標ですが、使い方の目的や場面が異なります。以下にそれぞれの特徴・メリット・デメリットを挙げます。
標準化得点(z得点)の 使い方・目的:
まず、標準化得点は「そのデータが集団の中でどの位置にあるか」を知りたいときに使われます。たとえば、数学のテストで80点、英語のテストで75点を取ったとします。このとき、単純に点数だけを見ても、どちらのテストで良い成績だったのかはわかりません。しかし、z得点を使えば、それぞれの平均点と標準偏差に基づいて、相対的な成績の良し悪しがわかります。平均点からどれだけ上にあるか、または下にあるかを標準偏差という共通の「ものさし」で測ることで、異なる種類のデータでも公平に比べることができます。つまり、z得点は「個別のデータが、その集団の中でどのくらい良いか悪いか」を判断するための指標です。
✔ 標準化得点のメリット:
- データが正規分布に近いときは、とても直感的(例:z = 2 なら「平均より2σ高い」)。
- 個別の点(値)が平均からどれだけ離れているかを明確に示せる。
- テストの点数の比較や、異なる評価軸をそろえるときに便利。
❌ 標準化得点のデメリット:
- 平均や標準偏差が0に近いと計算できない、または極端に大きくなる。
- 単純な「ばらつきの大きさの比較」には向かない。
- 多くのz得点をまとめて比較すると、集団ごとの分布特性を無視してしまう恐れがある。
変動係数(CV)の使い方・目的:
変動係数は、集団全体のデータの「ばらつき具合」を比較したいときに使います。こちらは、データのばらつきを表す標準偏差を平均で割って求めるため、「平均に対してどれくらい散らばっているか」を見ることができます。たとえば、商品の売上や体重、身長といった、単位や値の大きさが異なるデータでも、変動係数を使えば、どちらのデータのばらつきが相対的に大きいかを比べることができます。変動係数は、平均値が0に近い場合には使いにくいという注意点はありますが、測定の安定性や精度を評価する場面では非常に役立ちます。
✔ 変動係数のメリット:
- 単位やスケールが違っても、ばらつきの比較が可能。
- スコアの安定性や再現性の評価(信頼性)に広く使われる。 例:身長と体重、売上と利益など単位が異なる指標を比べるときに便利。
❌ 変動係数のデメリット:
- 平均値が0に近いと、変動係数が極端に大きくなり、意味を持たなくなる。
- データが負の値を含む場合は注意が必要(平均がマイナスだと直感的に解釈しづらい)。
- 「データの個別の位置」は示せない(z得点とは逆)。
実務での使い分け例:
- テストの得点を比べたい → z得点
- 商品の売上と在庫数のばらつきを比べたい → 変動係数
- 機器の計測値の安定性を評価したい → 変動係数
- 学力テストで自分の成績がどのくらいか見たい → z得点
四分位数と箱ひげ図って?
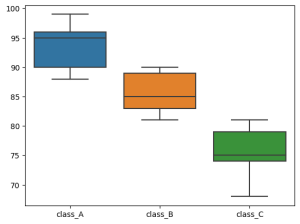
分布の特徴を順位情報をもとに把握するための指標として、四分位数および箱ひげ図があります。これらは外れ値や偏った分布において有効な記述手段です。
四分位数
データの分布を、順位に注目して見ていく方法です。
たとえば、データを小さい順に並べて、全体を4つに分けたときの区切りの値を四分位数といい、主に以下の5つの指標が用いられます:
- 最小値
- 第1四分位数(Q1):下位25%
- 中央値:50%
- 第3四分位数:上位25%
- 最大値
第1四分位数(Q1)は、データの下位25%の値の中間点を示し、第3四分位数(Q3)は上位25%の値の中間点を示します。この中でも、第1と第3の四分位数の間を「四分位範囲(IQR: Interquartile Range)」と呼び、データの中央50%がどれくらいの範囲にあるかを表しています。
Q3 - Q1 = IQR(四分位範囲)
箱ひげ図(Box-and-Whisker Plot)
そして、四分位数をわかりやすく図で表したのが箱ひげ図(boxplot)です。
箱ひげ図は、上記の四分位数を視覚的に表現した図で、以下の構成要素を持ちます。:
- 箱の下端:Q1
- 箱の中線:中央値
- 箱の上端:Q3
- ヒゲの端:Q1 - 1.5×IQR および Q3 + 1.5×IQR の範囲内の最小値・最大値
- 外れ値:ヒゲの範囲を超える値として点でプロット
例えば、以下のような偏ったデータがあったとしましょう。
12, 15, 15, 16, 18, 19, 20, 21, 22, 22, 25, 30, 35, 40, 60
このデータにおける四分位数は以下の通りです:
- 第1四分位数(Q1):16.0
- 中央値(Q2):21.0
- 第3四分位数(Q3): 30
- 四分位範囲(IQR):14
- 下限:Q1 − 1.5 × IQR = 16 − 21 = ‐5
- 上限:Q3 + 1.5 × IQR = 30 + 21 = 51
上限・下限を超える値(例:60)は外れ値として扱われることになります。
このデータを元にして箱ひげ図を描くと以下の図になります。
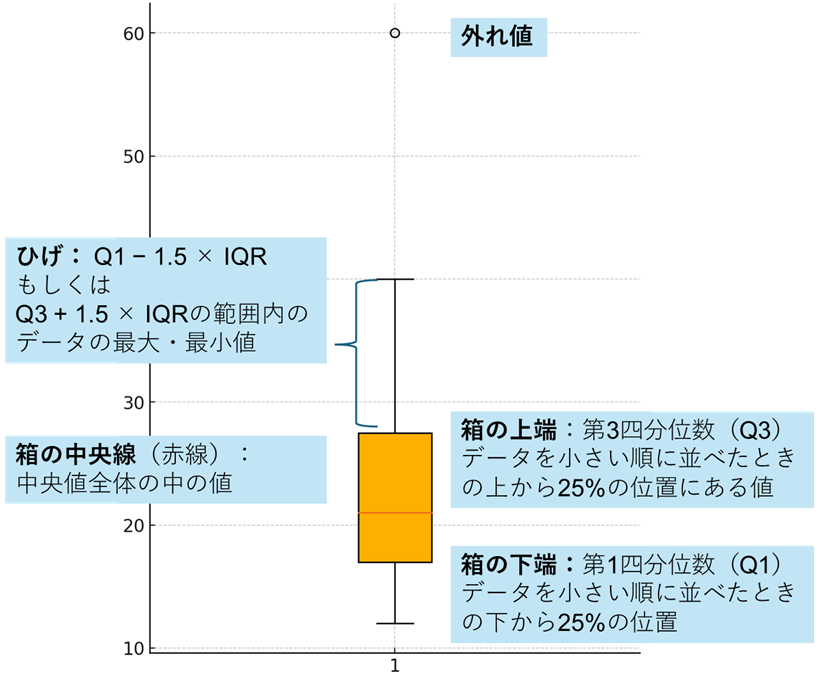
箱ひげ図を見ると、データのどのあたりに多くの値が集まっているか、左右に偏りがあるか、極端な値があるかがすぐにわかります。
たとえば、箱の真ん中に線があれば「真ん中付近にデータが多い」、箱の端が長く伸びていれば「広くばらついている」ことがわかります。
また、点がたくさんあると「外れ値が多い」こともわかります。
箱ひげ図なら、データの広がりや偏り、外れ値の有無を一目で確認できる、とても便利な図ですね。
まとめ

データの分布を理解するためには、「平均」や「標準偏差」などの指標を活用することが大切です。また、異なる種類のデータを比べたいときには、標準化得点(z得点)や変動係数が役に立ちます。
加えて、四分位数や箱ひげ図を使えば、データを順位の視点から捉えることができ、中心付近の分布や外れ値の有無を視覚的に把握することができます。
これらの指標を組み合わせることで、データの特徴をより多面的に理解することができるようになります。




コメント