一元配置分散分析 (One-way ANOVA) は3群以上の間で平均値に統計的に有意な差があるかどうかを調べるための統計手法です。
この記事はPythonを使って一元配置分散分析(One-way ANOVA)を簡単に行う方法を具体的なコード例を交えて説明していきます。Python初心者でも読み進めてもらえばStep-by-Stepで一元配置分散分析ができるようにまとめてみました。
必要なライブラリのインポート
ここでは、JupyterLabを使って解析します。ANOVAを実施するのに必要なライブラリーとして、"SciPy"の"stats"を使用します。
JupyterLabのインストール(必要な場合のみ)
もし、JupyterLabをインストールしていない場合は、まず、JupyterLabをインストールするために、以下のコマンドをコマンドラインに入力します:
pip install jupyterlabライブラリーのインストール
コマンドライン(ターミナル)を開いて、以下のコマンドを順に入力してライブラリーをインストールします。
pip install numpypip install scipyJupyterLabを起動
JupyterLabを起動するには、コマンドラインで以下のコマンドを実行します。
jupyter labコマンドを実行すると、Webブラウザが開き、JupyterLabのインターフェースが表示されるはずです。ここから新しいNotebookを作成して、数値計算や統計解析を行うことができます。
今回は、一元配置分散分析を行うために、以下のライブラリーをインポートします。
import pandas as pd
from scipy import statsサンプルデータの作成
一元配置分散分析で使うサンプルデータを作成します。今回は、3つの異なる群からのデータを仮想的に生成します。異なる3つの方法の得点だと考えてくださいね。
# サンプルデータの生成
data = {'Method_A': [85, 92, 88, 78, 95],
'Method_B': [76, 88, 82, 80, 78],
'Method_C': [90, 82, 88, 85, 92]}
# サンプルデータからデータフレーム作成
df = pd.DataFrame(data)上のサンプルデータは架空の方法(Method)A,B,Cの3群の得点結果です。これを変数名dfに代入してデータフレームを作成します。
No | Method_A | Method_B | Method_C |
|---|---|---|---|
| 0 | 85 | 76 | 90 |
| 1 | 92 | 88 | 82 |
| 2 | 88 | 82 | 88 |
| 3 | 78 | 80 | 85 |
| 4 | 95 | 78 | 92 |
一元配置分散分析(One way ANOVA)を実行
データを生成したら、一元配置分散分析を実行します。今回はPythonのscipy.statsモジュールに含まれるstats.f_onewayを使って一元配置分散分析を実行します。stats.f_onewayは、異なるグループの平均を比較して、それらが有意に異なるかどうか、あるいは同じかどうかを調べるのに役立ちます。
stats.f_onewayの使い方:
scipy.stats.f_oneway(samples)
※ samples: 各グループのサンプル測定値
詳細はstats.f_onewayの公式サイトを参照LINK: scipy.stats.f_oneway
今回のサンプルのような3つのグループ( 方法A、方法B、方法C)のデータを使って、「Method(方法)の違いが、テストの得点に影響を与えているのか、いないのかを知りたい」とします。
この時、stats.f_onewayは次のような解析を実行します。
① F統計量の計算: stats.f_onewayは、F統計量を計算します。もしF統計量が予想より大きければ、少なくとも1つのグループが他のグループと異なることを意味します。
② P値の計算: p値は「グループ間の差が本当にありそうなのか、それとも単なる偶然によるものなのか」を判断するのに役立つスコアのようなものです。p値が小さければ、その差は偶然によるものではないだろうということを示唆しています。
stats.f_onewayを使って一元配置分散分析を実行:
# One-Way ANOVAを実行
f_statistic, p_value = stats.f_oneway(df['Method_A'], df['Method_B'], df['Method_C'])
# 結果を表示
print("F値:", f_statistic)
print("P値:", p_value)出力結果は以下の様になります。
F-値 2.797011207970112
P-値: 0.10066920305785067
さらに、結果の判定をするコードを追加します。
# 結果の解釈
alpha = 0.05
if p_value < alpha:
print("帰無仮説を棄却。群間に統計学的な有意差があります")
else:
print("帰無仮説を棄却できません。群間には統計学的な有意差があるとはいえません")有意水準は0.05に設定しています。今回のP-値は0.10066920305785067なので、結果の解釈は、
帰無仮説を棄却できません。群間には統計学的な有意差があるとはいえません
となります。
(※ちなみにp値が低いほど、群間に有意差があることを示唆しています。しかし、低いp値だけでは、群間内のどの特定の群に差があるかはわかりません。どのグループが互いに有意に異なるかを決定するには、Tukey's HSDのような追加の事後検定が必要です。)
一元配置分散分析(ANOVA)の作図
箱ひげ図
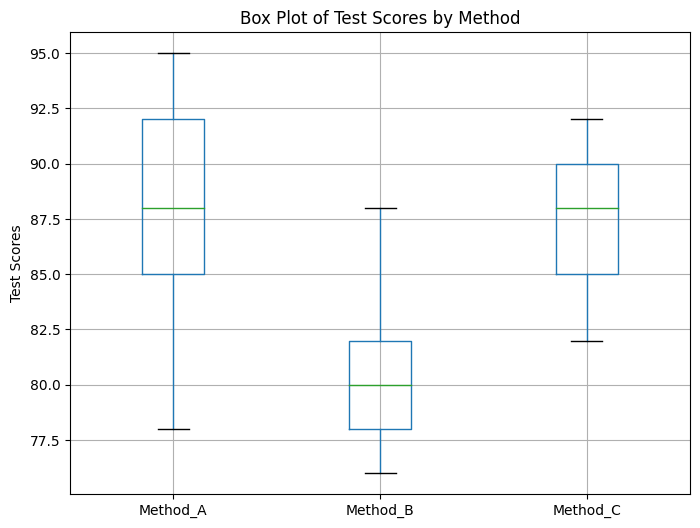
先ほどのANOVAの結果を図で示してみます。
まず、プロットを作成するためにmatplotlib.pyplotライブラリをインポートします。
import matplotlib.pyplot as plt
# 箱ひげ図
plt.figure(figsize=(8, 6))
df.boxplot()
plt.title('Box Plot of Test Scores by Method')
plt.ylabel('Test Scores')
plt.show()df.boxplot()を使って箱ひげ図を作成し、各方法のテストスコアの分布を可視化しています。
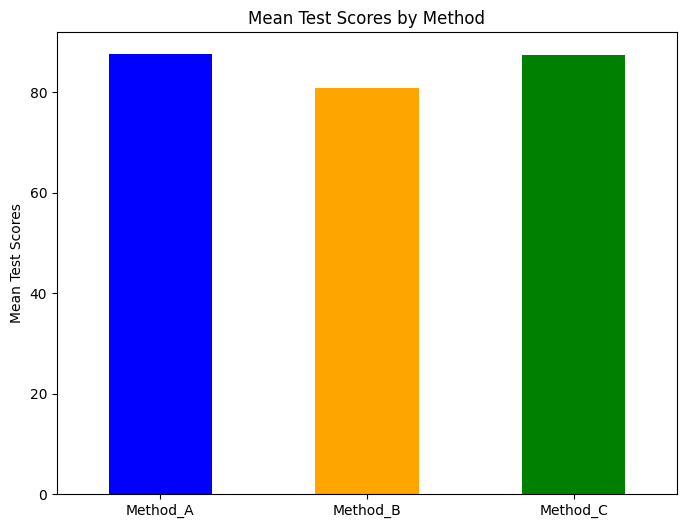
棒グラフ
続いて、棒グラフを作成します。
# 棒グラフ
plt.figure(figsize=(8, 6))
df.mean().plot(kind='bar', color=['blue', 'orange', 'green'])
plt.title('Mean Test Scores by Method')
plt.ylabel('Mean Test Scores')
plt.xticks(rotation=0)
plt.show()次はdf.mean().plot(kind='bar')を用いて、各メソッドの平均テストスコアを表示する棒グラフを作成します。また、読みやすくするために、プロットのタイトル、ラベル、X軸ラベルをカスタマイズします。
まとめ

一元配置分散分析は基本的な統計手法であり、複数のグループ間の差異を調査・分析するのに役立ちます。
scipy.stats.f_onewayのようなPythonライブラリーを利用することで、分析を行い、データを効果的に可視化し、統計的な証拠に基づいて情報に基づいた意思決定を行うことができます。




コメント