はじめに
量的(カテゴリー)データを対象とした研究論文では、アウトカム効果を示す尺度にオッズ比(OR)やリスク比(=相対リスク:RR)を用いています。
でも、オッズ比やリスク比はよく耳にしますが、しっかりと理解されていないことが多いので、今回はできるだけ簡単に嚙み砕いて説明していきます。
割合・比・率の理解
準備として「割合・比・率」について、おさらいおきます。
- 割合とは、「一部分を全体で割った値」
- つまり、分子は分母の一部
- 例えば、日本国民の女性の割合 = 女性人口 ÷ 全人口
- 比とは、「2つの値のを割った値」
- 分子と分母は別
- 例えば、男女比 = 男性人口 ÷ 女性人口

- 率とは「ある期間内に発生した特定のイベントの発生」
- 単位時間あたりの発生率
絶対リスク(ABSOLUTE RISK)
絶対リスクとは、あるリスク要因に暴露された群においてその事象が発生する可能性のことです。
絶対リスクの計算方法は、
実際に発生した人数 ÷ リスク要因に暴露された総数
$$相対リスク = \frac{A}{A + B}$$
で推定されます。
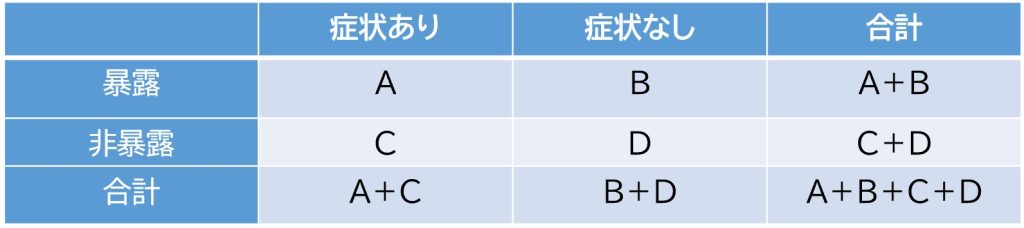
例えば、 A薬とプラセボの副作用(頭痛)発症について架空のデータが以下のようであった場合、
| 頭痛あり | 頭痛なし | 合計 | |
| A薬 | 10 | 40 | 50 |
| プラセボ | 5 | 45 | 50 |
| 合計 | 15 | 85 | 100 |
A薬を服用した50人中、10人が副作用として頭痛を発症しているので、
A薬による頭痛発症の絶対リスクは
$$\frac{10}{50} = 0.2$$
となり、A薬を投与された患者の20.0%が、投与後に頭痛を発症すると予想されます。
寄与危険(Attributable Risk)OR リスク差(Risk Difference)
寄与危険とは、リスク要因に曝露された人と曝露されていない人との絶対リスク差です。

$$寄与危険 = \frac{A}{A + B} - \frac{C}{C + D}$$
上のA薬とプラセボの例を使うと、「A薬による頭痛発症の絶対リスク」と「プラセボによる頭痛発症の絶対リスク」の差ですから、
| 頭痛あり | 頭痛なし | 合計 | |
| A薬 | 10 | 40 | 50 |
| プラセボ | 5 | 45 | 50 |
| 合計 | 15 | 85 | 100 |
$$\frac{10}{50} - \frac{5}{50} = 0.2 - 0.1 = 0.1$$
すなわち10%である。
この結果、A薬を投与された患者の20%が副作用として頭痛を発症すると予想されます。しかし、A薬に起因する頭痛発症は10%に過ぎず、残りの10%は他の要因が関与していると考えられます。
寄与危険割合(Attributable Risk Percent)
寄与危険割合とは、リスク要因に曝露された群で事象が発生した症例の内、特にリスク要因が起因する割合であり、

寄与危険 ÷ 絶対リスク
$$危険寄与割合 = \frac{\frac{A}{A +B}-\frac{C}{C + D}}{\frac{A}{A + B}}$$
で、求められる。
上のA薬とプラセボの例を使えば、
- A薬による頭痛発症の絶対リスク20.0%
- A薬による頭痛発症の寄与危険10.0%
つまり、A薬の寄与危険割合は、
$$\frac{0.1}{0.2} × 100 = 50$$
この結果を解釈すると、母集団で実際にA薬によって頭痛発症を認めた場合、その内の50%がA薬に起因する頭痛であり、残りの50%については他の要因が考えられるということです。
相対リスク(RELATIVE RISK)
相対リスクとは、リスク要因に曝露した群の罹患リスクと非暴露群の罹患リスクと比較したもので、リスク要因に暴露したことで
「どの程度(何倍)のリスクが増加したのか?」
を示します。
(暴露群の罹患者数 ÷ 暴露群の総数) ÷ (非暴露群の罹患者数 ÷ 非暴露群の総数)
=(暴露群の罹患リスク) ÷ (非暴露群の罹患リスク)

$$相対リスク = \frac{\frac{A}{A + B}}{\frac{C}{C + D}}$$
で、計算されます。
A薬とプラセボの例を使って相対リスクを計算すると、
| 頭痛あり | 頭痛なし | 合計 | |
| A薬 | 10 | 40 | 50 |
| プラセボ | 5 | 45 | 50 |
| 合計 | 15 | 85 | 100 |
$$\frac{\frac{10}{50}}{\frac{5}{50}} = \frac{0.2}{0.1} = 2$$
となります。
つまり、プラセボと比較して、A薬は頭痛発症のリスクを2.0倍増加させるということになります。
オッズ比(Odds Ratio)
オッズとは、
その事象が発生する回数(人数)÷ 発生しない回数(人数)
で表されます。
つまり、暴露群のオッズは、
$$\frac{\frac{A}{A + B}}{\frac{B}{A + B}} = \frac{A}{B}$$
さらに非暴露群のオッズは、
$$\frac{\frac{C}{C + D}}{\frac{D}{C + D}} = \frac{C}{D}$$

オッズ比の計算方法は、
(暴露群のオッズ) ÷ (非暴露群のオッズ)
$$\frac{\frac{A}{B}}{\frac{C}{D}} = \frac{AD}{BC}$$
A薬とプラセボの例を使うと、
| 頭痛あり | 頭痛なし | 合計 | |
| A薬 | 10 | 40 | 50 |
| プラセボ | 5 | 45 | 50 |
| 合計 | 15 | 85 | 100 |
$$\frac{\frac{10}{40}}{\frac{5}{45}} = \frac{10×45}{40×5} = 2.25$$
したがって、オッズ比は2.25となります。
結果として、A薬による頭痛発症のオッズ比はプラセボに対して2.25(対1)であると言えます。
注意!オッズ比から「A薬による頭痛発症はプラセボに対して2.25倍」は、
絶対にダメです!
ので、注意して下さい。
まとめ

今回はリスク比とオッズ比について、できるだけ実例を使いながら説明してみました。Rを使ったリスク比やオッズ比の求め方はまたの機会に詳しく説明しますね。


コメント