【10分あればOK】Rを使って信頼区間を求める方法

CONTENTS

推定値の信頼性？
平均値の信頼区間を求める
標本平均の信頼区間を求める
t分布から信頼区間を求める
R関数を使った信頼区間の求め方
まとめ

推定値の信頼性？

統計学を使って推定した値は実際どれだけの信頼性があるのでしょうか？

確率・統計の分野では、「大数の法則」や「中心極限定理」により、標本サイズが大きければ、

標本平均は母平均に近づく
標本平均の分布は、平均$\mu$、標準偏差$ \frac{σ}{\sqrt n} $に近似する

とされています。これを点推定といいます。しかし点推定には標準誤差があり標本平均と母平均が完全に一致するのは難しいことも事実です。特に標本サイズが小さい場合は標準誤差も大きくなります。

そこで点推定ではなく、一定の幅を持たせた推定値として区間推定があります。これは、まず集めたデータから統計量を計算し、その統計量を用いて母集団のパラメーターの上限と下限（一般的には95%）の信頼度を設定することで、一定範囲を持った推定量を求めることができます。これを信頼区間と呼びます。

平均値の信頼区間を求める

例えば、あるハンバーガーショップのフライドポテトMサイズの量について、お客様よりクレームがあったとします。

そこで、店長は20個のフライドポテトMサイズの量(g)を測定したところ、

135, 120.5, 142.5, 119.5, 137, 131.5, 151, 129.5, 152, 138.5, 134.5, 140, 119.5, 119, 132.5, 125.5, 150.5, 138, 136.5, 137

となりました。

では、まずは平均値と標準偏差を求めてみましょう。

potato <- c(135, 120.5, 142.5, 119.5, 137, 131.5, 151, 129.5, 152, 138.5, 134.5, 140, 119.5, 119, 132.5, 125.5, 150.5, 138, 136.5, 137)

mean(potato)
[1] 134.5

sd(potato)
[1] 10.20578

となり、平均値は134.5g、標準偏差は10.20578gということが分かりました。

標本平均の信頼区間を求める

では、今回のテーマである、この平均値がどのくらい信頼性があるかを求めてみましょう。

中心極限定理から「標本サイズが十分（30以上）であれば、標本平均の分布は正規分布に近似する」とされていますが、今回の標本サイズは20です。

つまり、標準誤差$ \frac{s}{\sqrt n} $が大きくなり、正規分布を使った検討はできません。

t分布から信頼区間を求める

そこで、母分散は未知で標本サイズが十分ではない場合、標本平均の分布はt分布を使用して推定することができます。

t分布の特徴としては、

正規分布と同様に左右対称の釣鐘形の形状の分布
範囲はー∞～∞
t分布の形状はパラメータである自由度(degree of freedom)によって変化する（下図参照）

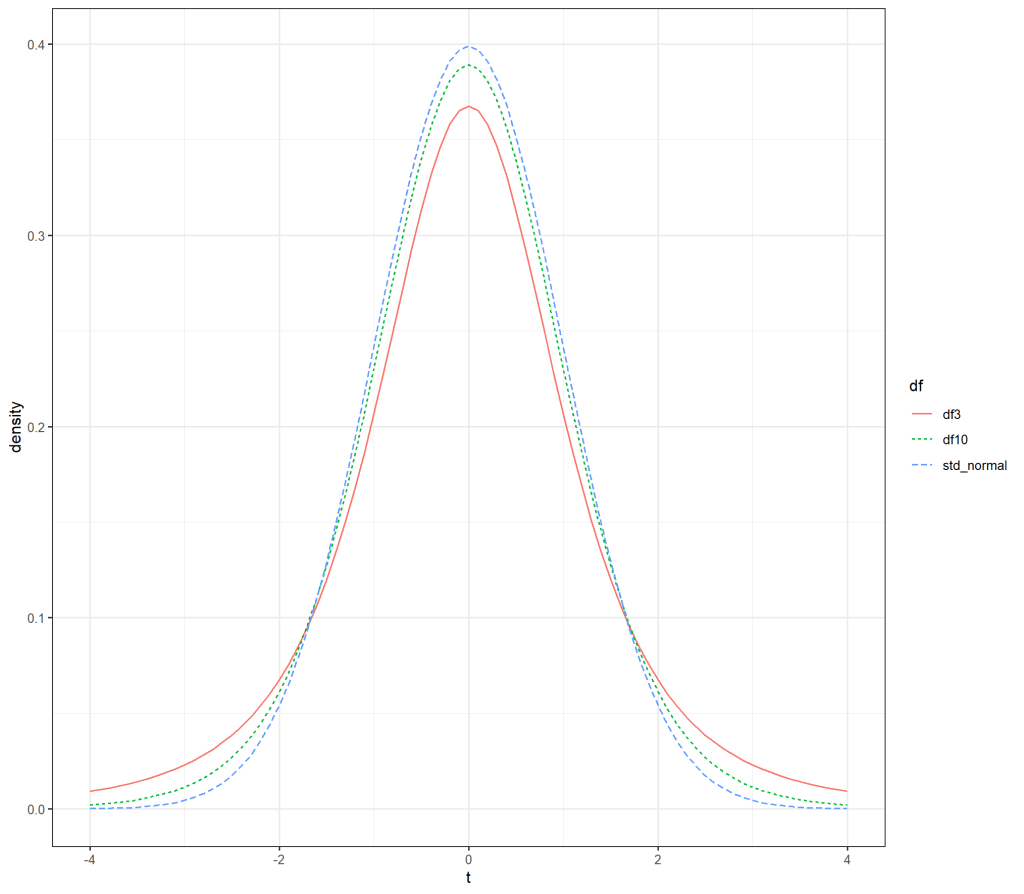
ｔ分布のパラメータは、自由度でdf＝N-1（Nはサンプルサイズ）

前置きが長くなりましたが、実際に、t分布を使った標本の95％信頼区間の下限と上限を求めてみます。

まず信頼区間の理解を深めるために公式に沿って信頼区間を求めてみましょう。

$$\bar{x} - t_{\frac{α}{2}} \times \frac{s}{\sqrt{n}} \lt \mu \lt \bar{x} + t_{\frac{s}{2}} \times \frac{σ}{\sqrt{n}}$$

両側なので、95%信頼区間の場合は"α = 0.025"となります。

正規分布の際に触れましたが、Ｒでt分布を扱うためのd○○()（密度関数）、p○○()（累積密度関数）、q○○()（分位点）、r○○()（乱数生成）があり、信頼区間はqt()を使っています。

統計量(t) は、

qt(.025,20-1,lower.tail=FALSE)
[1] 2.093024

となりました。そこで、これまで把握している数値（平均値・標準偏差・標本数）を入れて、上限・下限を求めましょう。

mean_potato <- 134.5
sd_potato <-  10.20578
N <- 20
error <- qt(.025, 20-1, lower.tail = FALSE)*sd(potato)/sqrt(N)
lower_limit <- mean_potato - error
upper_limit <- mean_potato + error
lower_limit
[1] 129.7235
upper_limit
[1] 139.2765

となり、95%信頼区間の

上限信頼限界＝139.2765
下限信頼限界＝129.7235

ということが分かりました。

R関数を使った信頼区間の求め方

信頼区間を一瞬で求めるには

信頼区間を理解していただくために、少し回りくどい求め方をしましたが、実際はもっと簡単にRで求めることができます。

それは、t.test()関数を使います。

t.test(potato)

と入力すると、結果は以下のようになります。

One Sample t-test
data: potato
t = 58.937, df = 19, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
129.7235 139.2765
sample estimates:
mean of x
134.5

と、黄色でハイライトした箇所に95%信頼区間が表示されています。