平均値(mean)
「平均値」は、日常に溢れています。身長や体重の平均値、平均収入・平均点・平均売上…etc。なぜなら、平均値は、とても手軽にデータをまとめてくれる数字だからです。

そして医学分野においても、治療の効果や全体との比較に平均値を使用します。
平均値とは、「データの総和÷テータの個数」ですね。
これを数学的に表すと
$$\bar{x} = \frac{\sum x}{N}$$
と表されます。
Rで平均値を計算する
平均値は英語ではmeanと言います。ですから、Rで平均値を計算する関数は、「mean関数」を使います。
例えば、6人の身長(heights)の平均値を求める場合、
heights <- c(165, 142, 170, 159, 153, 161)
mean(heights)
[1] 158.3333
と、158.3333cmになります。
また、複数の項目を含んだデータ(データフレーム)の1項目(つまり特定の列)を選択して平均値を求める場合も多いですね。
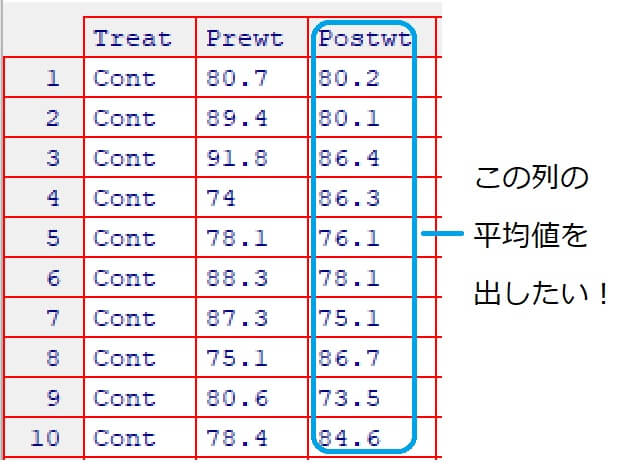
上記のような場合は「mean関数」と「with関数」を合わせて使います。
例としてRのMASSパッケージにあるanorexiaデータを使って解説します。
まずは、libraryからMASSパッケージを読み込みます。
library(MASS)
次に、MASSパッケージ内に含まれるanorexia(拒食症)データのPrewt(治療前の体重)とPostwt(治療後の体重)の平均値を求めてみます。
with(anorexia, mean(Prewt))
[1] 82.40833
with(anorexia, mean(Postwt))
[1] 85.17222
これで、拒食症(anorexia)の治療によって、患者の治療前後の平均体重は増加したことが解りますね。
Rで中央値(median)を計算する
平均値は中央値や最頻値と比較すると、外れ値の影響を大きく受けてしまう性質があることは承知のとおりです。
一方、中央値とは、データを順番(大きい順OR小さい順)に並べたときの中間点の値をいい、外れ値の影響を受けにくいのが特徴です。
Rで中央値を計算するには「median関数」を使います。
例としてmedian.exに以下の値を代入し、sort関数にて小→大の順で並べてみます。
median.ex <- c(56, 78, 45, 49, 62)
sort(median.ex)
[1] 45 49 56 62 78
上の[1]の結果を見ると、中央値は真ん中の「56」になります。
実際に、Rのmedian関数を使ってみると、
median(median.ex)
[1] 56
「56」になりましたね。
もし、データ数が偶数で中央の値が2つになる場合はその平均値をとります。
median.ex2 <- c(56, 78, 45, 49, 62, 55)
sort(median.ex2)
[1] 45 49 55 56 62 78
median(median.ex2)
[1] 55.5
この場合は、55と56が中央になるので平均をとって中央値は55.5となります。


コメント