平均値と言えは、集めたデータを全て足した合計をデータ数で割る、
$$\frac{(x_1 +x_2 + ... +x_n)}{n}$$
を思い浮かべますね。
この平均値は算術平均と呼ばれます。
統計学ではさらにノンパラメトリックやカテゴリーデータ等で使用される中央値も平均値の1つです。

が、
この代表的な2つ以外にも様々な平均値が適切な場面において算術平均以上の代表値と成り得ます。
そこで、今回は様々な平均値とその使い方を紹介します。
最頻値(mode)
読んで字のごとく最も頻繫に発生する値を代表値する方法です。
例えば、国民生活基礎調査結果の概要より、所得金額の相対度数分布を見ると、
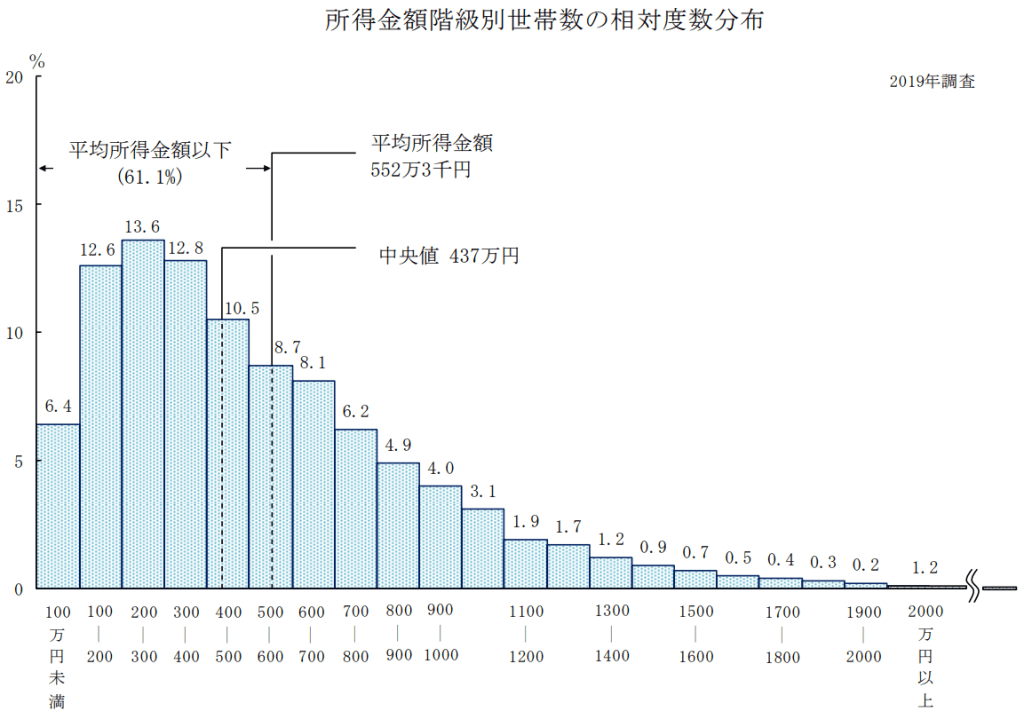
年収200-300万円が最頻値と読み取ることができます。
最頻値の特徴として、中央値同様に外れ値の影響を受けにくいことですね。(算術平均では552万3千円となっていますが、これは、一握りの高額所得者の外れ値データに引っ張られている結果です)
一方で、最頻値の短所としては、最頻値が1つとは限らないということです。データによっては2以上の最頻値が発生してしまうと、どれを代表値とするのか不明ですね。
加重平均(weighted mean)
加重平均は各データ毎に重みづけを行って平均をとる方法です。
公式は:
$$\frac{w_1x_1 + w_2x_2 + ... + w_nx_n}{w_1 + w_2 + ... +w_n}$$
例えばクラスのテスト配分が以下のようなWeightで配分され、平均70点が合格ラインであった場合を考えてみます。
| テスト | 加重(weight) | テスト結果(100点満点中) |
| 小テスト1 | 10% | 50 |
| 小テスト2 | 10% | 65 |
| 中間テスト | 25% | 75 |
| 小テスト3 | 10% | 50 |
| 期末テスト | 45% | 80 |
この場合、最終的な平均点は
$$\frac{0.1×50+0.1×65+0.25×75+0.1×50+0.45×80}{0.1+0.1+0.25+0.1+0.45} $$
= 71.25点ですね。
つまり、このクラスなら配分の少ない小テストで成績が振るわなくても中間・期末テストを頑張れば大丈夫ですね😉!
幾何平均(相乗平均)
幾何平均は主に変化率の平均をとる場合に用いられる平均です。
公式は:
$$\sqrt[n]{x_1 × x_2 × ... × x_n}$$
例えば、ある会社の3年間の売り上げが前年比の10%→25%→20%と毎年好調に伸びているとします。
| 年 | 伸び率(前年比) |
| 2年目 | 10% (=1.10) |
| 3年目 | 25% (=1.25) |
| 4年目 | 20% (1.20) |
この会社の平均の伸び率は
$$\sqrt[3]{1.10 × 1.25 × 1.20}$$
= 1.181666
つまり、平均18.17%の伸び率ということになる。
また、
$$x_n = (1 + g)^n × x_0$$
で基準の年(x0)、平均増加率(g)とすると、n年後にどのくらいの値となるかを予測できます。
さらに、この式を変形して
$$n = \frac{\log_{10} (x_n/x_0)}{\log_{10} (1 + g)}$$
とすれば、目標の値(xn)までに何年(n)必要かも平均増加率(g)が分かれば予想することもできます。
調和平均(Harmonic mean)
スピード等の「率」を平均する時に使用されます。

公式は、
$$\frac{1}{\frac{1}{n}(\frac{1}{x_1} + \frac{1}{x_2} + ... + \frac{1}{x_n})}$$
例えば、朝の自家用車で通勤する時は45㎞/hであったが、帰りは急用があったので65㎞/hで戻ってきた場合、その日の平均時速を求めたければ
$$\frac{1}{\frac{1}{2}(\frac{1}{45} + \frac{1}{65})}$$
=53.18182
となり、53.18㎞/hが平均スピードとなります。
計算もわかりにくいので、Rで簡単に求めちゃいましょう!
x <- c(45, 65)
hm.mean <- 1/mean(1/x)
hm.mean
[1] 53.18182
トリム平均
例えば外れ値があって、その影響を取り除くために両端の数%を削除して外れ値の影響を除いて平均をとる方法で。外れ値を取り除いたら、通常の算術平均と同様の方法で平均を求めます。
こちらもRには引数の”trim =”を応用すれば簡単です。例えば、
x <- c(45,52,60,39,55,62,59,98,42,61)
mean(x)
[1] 57.3
mean(x, trim = 0.1)
[1] 54.5
と、いう風に両端10%(39と98)をトリムして平均してくれています。
移動平均
奇数項での移動平均が分かりやすく
- 3項移動平均
- 5項移動平均
偶数項でも
- 四半期データ:中心化4項移動平均
- 月次データ:中心化12項移動平均
等もあります。
移動平均については別の記事で詳しく説明します。
まとめ
今回は様々な平均値についてまとめてみました。
いつでも算術平均を使うと、データの解釈に誤りがあることが理解して頂いて、適切なケースで適切な平均値を求めてデータ分析をして頂ければと思っています。




コメント