データの標準化(Z‐スコア)はt検定やANOVA、相関、回帰分析などのデータ分析において用いられる統計学における重要なコンセプトの一つです。

Z‐スコアとは
”(データー平均値)÷標準偏差”
で求めることができます。公式で書くと以下のようになります。
$$Z = \frac{x - \bar{x}}{σ} (母集団)$$
$$Z = \frac{x - \bar{x}}{s} (標本)$$
上記の式からも推測できますが、Z‐スコアは平均が0、標準偏差が1です。
例えば、あるシニアクラブのメンバー10人の年齢が以下のようであった場合、
| id | age | mean | sd | z_score |
| 1 | 69 | 75.5 | 5.77 | (69 - 75.5) / 5.77 = -1.13 |
| 2 | 74 | 75.5 | 5.77 | -0.26 |
| 3 | 76 | 75.5 | 5.77 | 0.09 |
| 4 | 70 | 75.5 | 5.77 | -0.95 |
| 5 | 82 | 75.5 | 5.77 | 1.13 |
| 6 | 86 | 75.5 | 5.77 | 1.82 |
| 7 | 67 | 75.5 | 5.77 | -1.47 |
| 8 | 80 | 75.5 | 5.77 | 0.78 |
| 9 | 78 | 75.5 | 5.77 | 0.43 |
| 10 | 73 | 75.5 | 5.77 | -0.43 |
Z‐スコアは一番右の列のようになります。
つまり、Z‐スコアが0に近い人ほど平均(75.5歳)に近い年齢となります。
また、±1以上だと±1標準偏差(5.77年)以上平均年齢より離れているということです。(±2以上なら、±2標準偏差以上、…)。
上記の例では、Z-スコアが1.82がプラスで最も大きく86歳、マイナスはー1.47で67歳ですね。
RでZ‐スコアを計算:scale関数
RでZ‐スコアを計算する場合、scale関数を使用すれば簡単にできますよ。
例えば、上のシルバークラブ10人の年齢を使うと、
age_std <- c(69, 74, 76, 70, 82, 86, 67, 80, 78, 73)
scale(age_std)
[,1]
[1,] -1.06939657
[2,] -0.24678382
[3,] 0.08226127
[4,] -0.90487402
[5,] 1.06939657
[6,] 1.72748677
[7,] -1.39844167
[8,] 0.74035147
[9,] 0.41130637
[10,] -0.41130637
attr(,"scaled:center")
[1] 75.5
attr(,"scaled:scale")
[1] 6.078194
という風に、各データのZ‐スコアが得られました。
Z‐スコアの下にattr(,"scaled:center")とありますが、これはデータの平均値です。
また、attr(,"scaled:scale")とは、標準偏差ですが、上の表の結果(5.77)と異なる結果(6.078)となっています。これは、Rでは不偏分散から求められている「母標準偏差の不偏推定量」であるからということを覚えておいてください。
まとめ
では、今回は、Rでデータの標準化を行うscale関数についてまとめました。


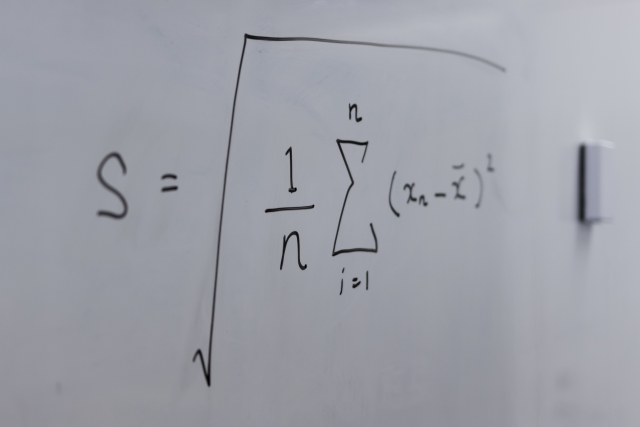
コメント