今回は「成功か失敗」、「有る・無し」の確率を扱う二項分布について統計初心者の方でも簡単に理解できるようにまとめます!
ベルヌーイ試行
まず二項分布を理解するために必要な、ベルヌーイ試行から始めます。ベルヌーイ試行は、「成功か失敗」、「有る・無し」等、結果が2種類である試行をいい、以下のような特徴があります。
- n回の繰り返し試行
- 各試行結果は成功/失敗等の2つだけ
- 成功確率(p)は各試行で一定
- 各試行は独立である。
ベルヌーイ試行の例として最も一般的なものは「コイン投げ」です。
例えば、コイン投げを10回、繰り返したとします。
この10回のコイン投げは、
- 10回の繰り返し試行
- 試行結果は表/裏の2つ
- 「表」を成功とすれば、成功確率は0.5
- 各試行(コイン投げ)は他の試行に影響しない=独立である
よって、コイン投げはベルヌーイ試行となります。
二項分布
では、本題の二項分布です。
二項分布は、n回のベルヌーイ試行でk回の成功が得られる確率を表します。
確率変数Xが二項分布に従うとすると、X=k回成功する確率は、次の式で求められる。
$$P(X=k) = {_n \mathrm{C}_r} p^k (1-p)^{n-k}$$
- n: 試行回数
- k: 成功の数
- p: 与えられた試行で成功する確率
- nCk: n回の試行でk回成功する方法の数
例えば、コインを10回投げた時、表が4回、8回出る確率は、上の式を使うと、
$$P(X=4) = {_{10} \mathrm{C}_4} (0.5)^4 (1-0.5)^6 = 0.205$$
$$P(X=8) = {_{10} \mathrm{C}_8} (0.5)^8 (1-0.5)^2 = 0.0439$$
となります。
二項分布のグラフを作成
では、上のコイン投げ10回の二項分布をグラフに表してみます。
グラフ作成はRに任せてしまいましょう。
Rのdbinom()関数を使えば、簡単に二項分布のグラフを作成できます。
まず、コイン投げを10回行ったときに表の出る回数を、
n_head <- seq(0,10)
とします。つぎに、コイン投げ10回で表が1~10回出る確率を求めます。
probability <- dbinom(n_head,10,1/2)
上のn_headとprobabilityをベースにggplot2でグラフを作成します。
library(ggplot2)
ggplot(NULL,aes(x=n_head,y=probability)) + geom_bar(stat="identity",width=1,color="white", fill = "blue")
すると、下図が結果です。
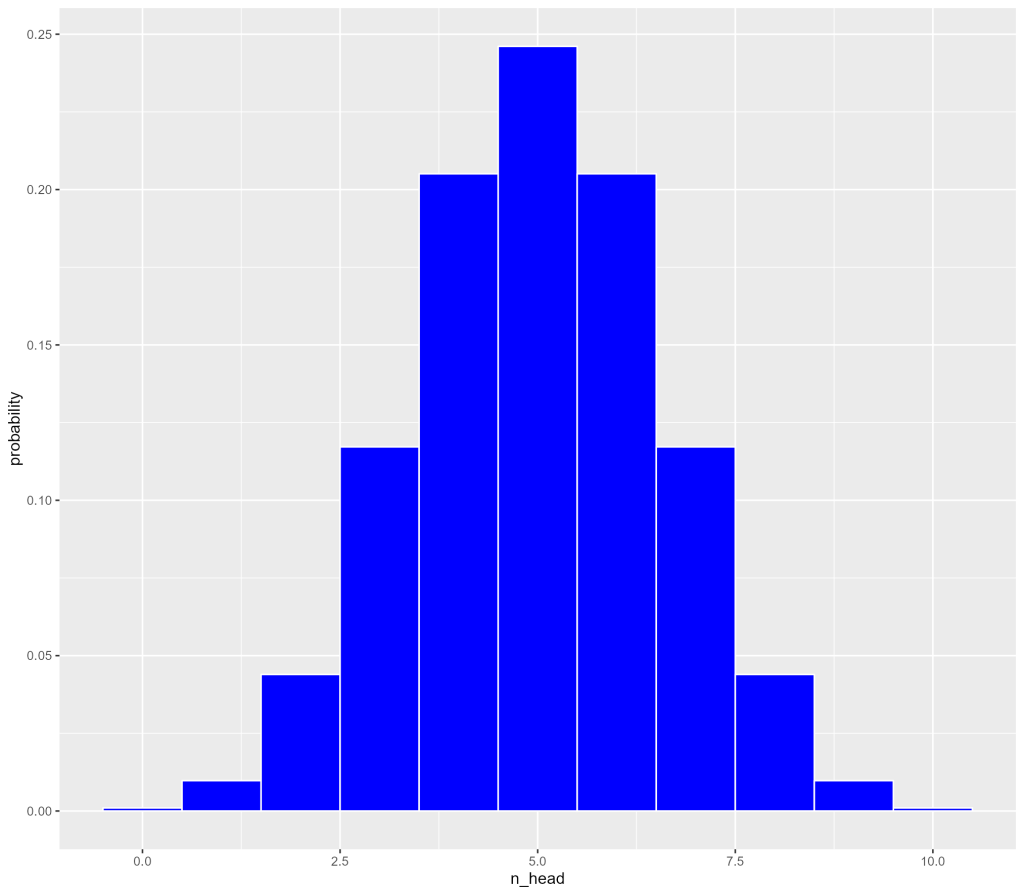
この二項分布のグラフから、コイン投げ10回で表の出る回数は、
- 5回の時の確率が最高
- 5回以上、あるいは、5回以下になるにつれて、確率が低下傾向
が分かります。
二項分布の性質
二項分布は、次のような性質を持っています。
- 分布の期待値:$$μ = np$$
- 分布の分散:$$σ^2 = np(1-p)$$
- 分布の標準偏差:$$σ = \sqrt{np(1-p)}$$
例えば、コイン投げを10回した時の、表が出る確率をPとします。
- 期待値\(μ = np = 10 × 0.5 = 5\)
- 分散は\(σ^2 = np(1-p) = 10 × 0.5 × (1-0.5) = 0.25\)
となります。
Rを使って二項分布を分析:dbinom, pbinom, qbinom, rbinom
Rで二項分布の分析を行うには、dbinom、pbinom、qbinom、rbinom関数を使います。
dbinom関数
dbinomは、ある確率変数x、試行回数(size)、各試行での確率(prob)が与えられたときの二項分布の確率密度関数の値。つまり、成功回数x回の確率を求めます。
dbinom(x, size, prob)
例えば、コインを10回投げた時、表が5回出る確率は、
dbinom(5,10,0.5)
[1] 0.2460938
で、24.6%です。
(先に示した棒グラフでも表が出る確率を確認できますね。)
また、複数の確率を求めることも可能で、上の条件で、表が3、7、9回でる確率は、
dbinom(c(3,7,9), 10, 0.5)
[1] 0.117187500 0.117187500 0.009765625
となります。
pbinom関数
pbinom関数は、ある確率変数q,試行回数(size),各試行の成功確率(prob)が与えられたときの,二項分布の累積密度関数の値、つまり、q回以下の確率を求めます。
pbinom(q, size, prob, lower.tail = TRUE)
q回以下の確率ですから、pbinomは二項分布における与えられた値qの左側の面積を返します。
もし、与えられた値qの右側(つまりq回以上)の領域に興味があるなら、引数lower.tail = FALSEを追加します。
例えば、コインを10回投げた時、表が出る回数が5回以下の確率(つまり、表が0回+1回+2回+3回+4回+5回出る確率)は
pbinom(5, 10, 0.5)
[1] 0.6230469
で、62.3%です。
qbinom関数
qbinom関数は、ある確率変数 p、試行回数 (size)、各試行の成功確率 (prob) が与えられたとき、二項分布の累積密度関数の逆関数の値、つまり、二項分布 p の分位数を求めます。
qbinom(p, size, prob)
例えば、コインを10回投げた時、表が出る累積確率が60%となる成功回数はn回以下であるかを求めるには、
qbinom(0.6, 10, 0.5)
[1] 5
ちなみに10回中、表が4回および6回出る累積確率は以下の通りです。
pbinom(c(4,6), 10, 0.5)
[1] 0.3769531 0.8281250
表が4回以下なら37.7%、6回以下なら82.8%ですね。
rbinom関数
rbinom関数はベクトル(n)、試行回数 (size)、各試行の成功確率 (prob) を与えると、二項分布の確率変数のベクトルを生成、つまりに二項分布からランダムサンプリングをn個生成します
rbinom(n, size, prob)
例えば、コインを10回投げた時、表が出る回数をランダムサンプリングすると以下のような結果となります。(※ランダムですので、結果は毎回、異なります。)
rbinom(5, 10, 0.5)
[1] 5 7 4 6 3
まとめ

今回は二項分布について初心者の方でも分かるようにまとめてみました。また、Rを使ったdbinom/pbinom/qbinom/rbinom関数についても紹介しましたので、是非、試してみてください。




コメント