R初心者でもOK！単回帰分析とlm関数を分かりやすく説明します

CONTENTS

単回帰分析とは
単回帰直線の公式
Rによる単回帰分析
回帰直線の見方
回帰直線で予測
決定係数
まとめ

単回帰分析とは

単回帰分析は、2つの変数間の関係を要約して調べることができる統計手法です。このとき、

ｘ軸：予測変数・説明変数・独立変数
ｙ軸：応答変数・結果変数・従属変数

と呼ばれます。

今回の説明では、ｘを「予測変数」、ｙを「応答変数」とします。

単回帰分析では、1つの予測変数のみのを扱うので、「単」という形容詞がつきます。一方、2つ以上の予測変数が関わる場合は「重」がついて、重回帰分析と呼ばれます。（※重回帰分析についてはまた別の機会に説明します。）

例えば、以下のような体重と身長データセットある時、xを体重、yを身長として散布図を書くと以下のようになります。

weight（㎏）	height（㎝）
64	160
62	164
59	160.5
60	158
41	148
48	157
50	151.8
53.5	151.2
36	144.8

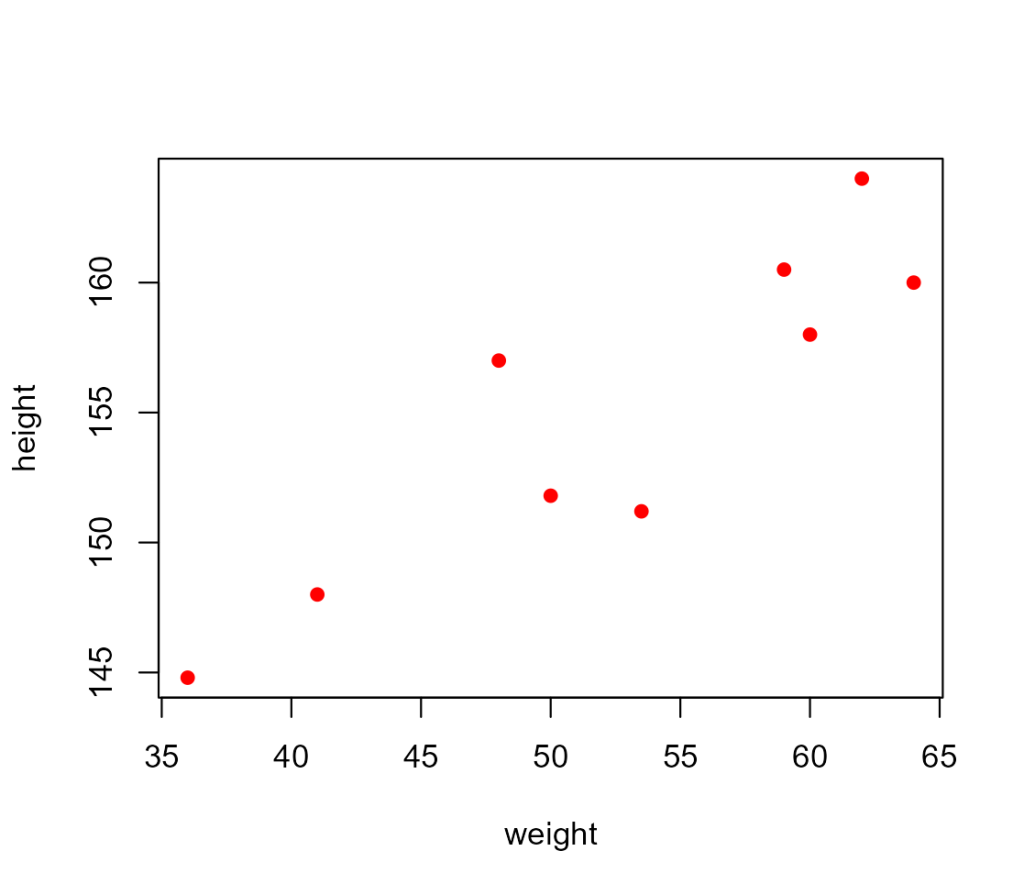
この散布図から、体重が増加すると身長も増加する傾向があることが予測できますが、この傾向を実際に数値化したのが、単回帰直線です。

単回帰直線の公式

単回帰分析を使うことで散布図上の全データに最も「フィット」する直線を見つけることができます。さらに、この直線から体重と身長の関係を理解することが可能となります。

回帰直線の一般式

$$ý = a + bx$$

$$b =\frac{\sum(x - \bar{x})(y-\bar{y})}{\sum(x -\bar{x})^2}$$

$$a = \bar{y} - b\bar{x}$$

Rによる単回帰分析

上の公式を使っても単回帰直線を求めることは可能ですが、やはりRを使えば単回帰直線以外も分析も一発に解析できるのでお勧めします。
では、lm()関数を使って回帰直線を求めてみます。

まず、上の例をデータフレームの形にします。

weight <- c(64.0,62.0,59.0,60.0,41.0,48.0,50.0,53.5,36.0)
height <- c(160.0,164.0,160.5,158.0,148.0,157.0,151.8,151.2,144.8)
w_h <- data.frame(weight, height)

これで、上の例のデータフレームができました。では、lm()関数の出番です。

lm(応答変数~予測変数, data = データフレーム名)が一般的な形式です。
そして、summary()関数で詳細を表示させます。

w_h.reg <- lm(height ~ weight, data = w_h)
summary(w_h.reg)

すると、結果は以下のようになります。

Call:
lm(formula = height ~ weight, data = w_h)

Residuals:
Min 1Q Median 3Q Max
-4.3590 -1.6893 -0.4104 1.6886 4.6934

Coefficients:
　　　　　 Estimate 　Std. Error 　t value　 Pr(>|t|)
(Intercept) 123.9220 　5.8701 　　21.111 　1.35e-07 ***
weight 　　0.5913　　0.1099　　 5.379　　 0.00103 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.016 on 7 degrees of freedom
Multiple R-squared: 0.8052, Adjusted R-squared: 0.7774
F-statistic: 28.94 on 1 and 7 DF, p-value: 0.001031