Rを使った歪度・尖度の解釈や求め方を初心者の方でもわかりやすく解説します。例題を使ったskewness関数やkurtosis関数の方法を解説します。
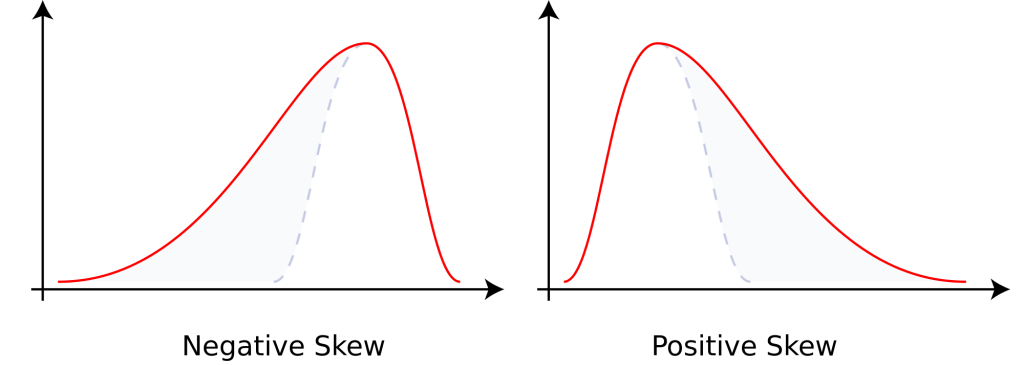
歪度 (skewness)
歪度とは分布の左右対称性を見るための指標として求められます。
歪度は以下のポイントが重要です。
- 歪度が正の値:分布は右に歪んだ(右に伸びた)分布
- 歪度が負の値:分布は左に歪んだ(左に伸びた)分布
- 歪度が0:完全に左右対称→現実のデータ分析では起こりうることはほぼ無いと思われますが…
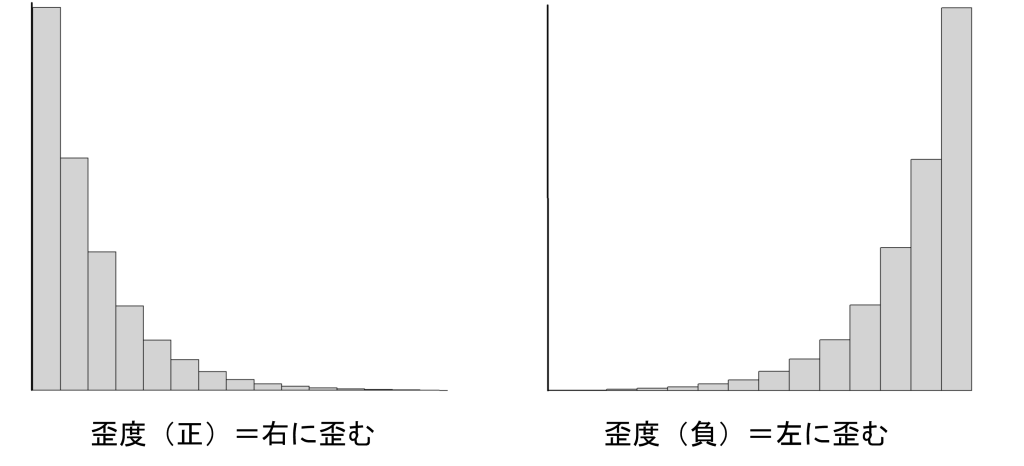
ところで、Rの基本設定(Base R) では、歪度を求めることは簡単にはできません。
(※歪度の公式をRに入力すれば計算することは可能ですが…、ちょっと手間)
でも、"momentsパッケージ"を使用すれば簡単に歪度(ちなみに尖度も)が求められます。
momentsパッケージインストール
まずはパッケージのインストールとlibraryで"momentsパッケージ"を使用できるようにします。
install.packages("moments")
library(moments)
これで、"momentsパッケージ"を使用することができるようになりました。
サンプルデータとして、上の図で示した歪度のデータを使用します。
set.seed(5)
rt_skewed <- rbeta(100000,1,100)*10 #分布が右に歪むデータ
lt_skewed <- rbeta(100000,100,1)*10 #分布が左に歪むデータ
歪度の計算
歪度を求める関数はskewness( )です。
skewness(rt_skewed)
[1] 1.946581
skewness(lt_skewed)
[1] -1.924689
ということで、無事に歪度を求めることができました!
歪度が正なら右に歪み、負なら左に歪んだ分布となっていますね。
尖度(kurtosis)
歪度のところでも説明しましたが、尖度も"momentsパッケージ"を使用することで、簡単に求めることができます。

尖度は、正規分布と比較してどれくらい「尖っているのか」を見る指標です。言い換えれば、「分布のバラつき度合い」を見る指標です。
尖度のポイント
以下のポイントが尖度を考えるときには重要です。
- まず最重要なのが、「尖度‐3」と尖度の値から3を引き算します!そして得られた値を、以下の基準で考えてください。
- 尖度が正の値:正規分布と比べて尖った分布=データのバラつきが少ない
- 尖度が負の値:正規分布と比べて平らな分布=データのバラつきが大きい
- 尖度が0:正規分布
尖度の例題
例えば、テストの結果が以下のようであった場合、
test_score<- c(46, 46, 49, 49, 49, 49, 49, 49, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 50, 52, 52, 52, 52, 52, 52, 55)
グラフを描くと以下のようになり50点に集中していますね。
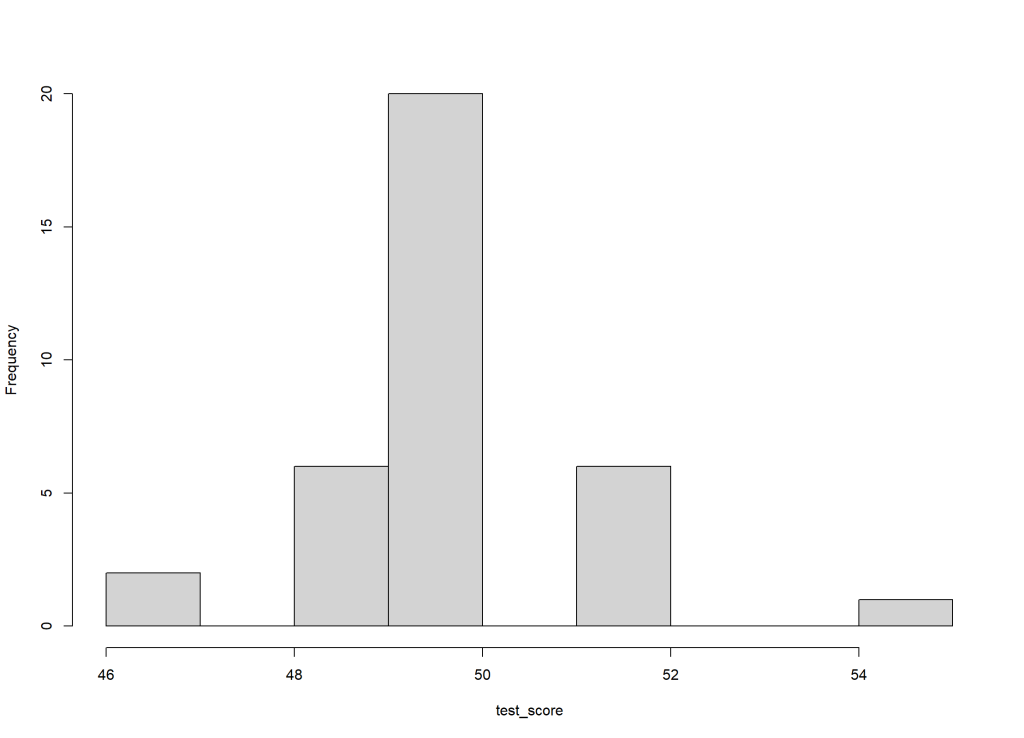
では、実際に歪度を求めてみましょう!
kurtosis(test_score)
[1] 5.718924
尖度は5.718924ですので3を引き算しても正の値ですから、正規分布よりも尖った分布となっていることが数的にも把握できます!



コメント