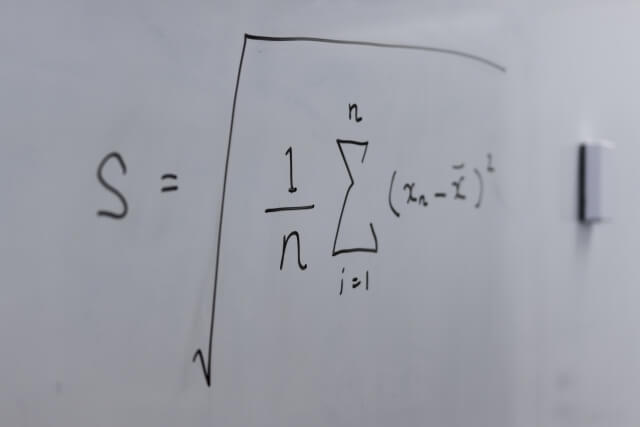
分散
例えば、ある2つの学校の生徒同士が話をしているのが偶然聞こえてきたとします。
A: 期末テストの数学、平均50点中で72点だったよ。
B: 私も平均50点中で72点だったよ。同じだね~。
この会話を聞くと、2人の学力は同じように聞こえます。
しかし、もし、それぞれの学校の数学の期末テスト結果が以下のようであったらどうでしょうか?
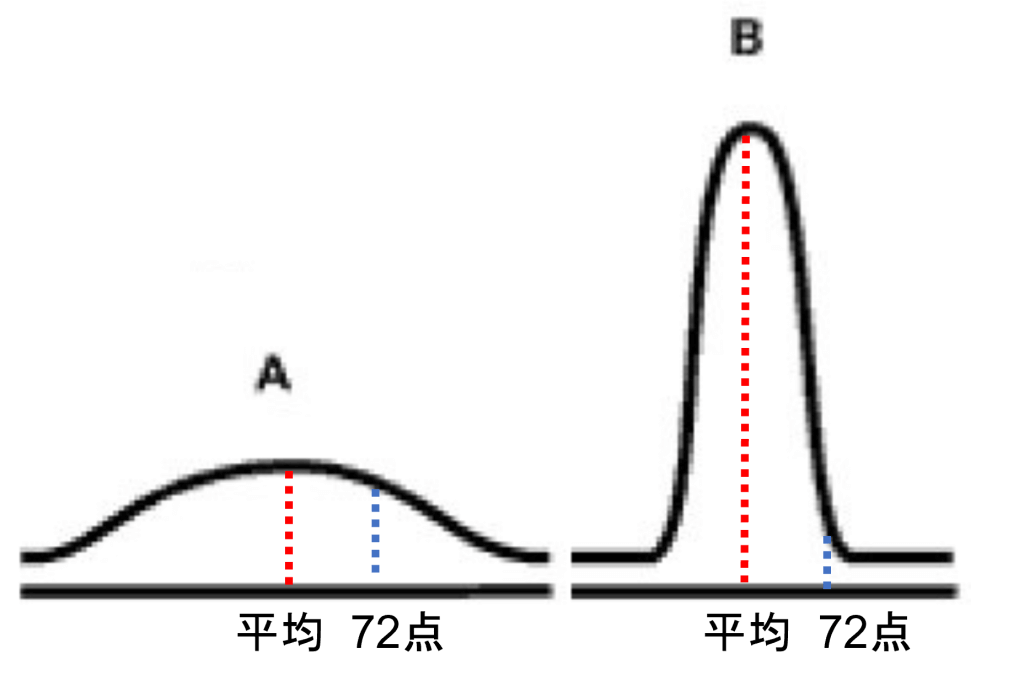
同じ平均点50点としても、Aの学校では平均点周囲のバラつきが大きく、Aは学校でも真ん中より少し上位といった感じですね。
一方、Bの学校では大半の生徒が平均点(50点)の周囲に集中しており、同じ72点でもBは学校内ではかなり上位のトップレベルに位置していることが分かります。
つまり、純粋なデータの値のみで比較検討することで、解釈を誤る危険であることが理解できます。
そこで、今回はこのバラつきを表す「分散」と「標準偏差」について、そしてRを使った分散(var)と標準偏差(sd)の求め方について解説します。
分散とその計算方法
2群間を比較する方法の一つとして分散を見る方法があります。
分散とは「平均値からのズレ」だと考えてください。
しかし、単純にこのズレを(実測値ー平均値)で求めて合計すると、ゼロになってしまいます(実際に試してみるとわかりますよ)。
そこで分散を計算するには、(実測値ー平均値)2して総和を求めた後、個数(N)で割ります。
以下に一般的な公式を示します。
$$σ^2 = \frac{\sum(x - \bar{x})^2}{N}$$
分散が大きいとデータは平均値からのバラつきが「大きく」、分散が小さいとデータは平均値からのバラつきが「小さい」と判断できます。
上記の公式は母集団の分散を求めるものです。
しかし、一般に臨床では標本データから母集団を推測することとが殆どですから、標本データを元に母集団の分散を推測する(これを不偏分散といいます)場合は、以下の公式を使用します。
$$s^2 = \frac{\sum(x - \bar{x})^2}{N-1}$$
Rを使った分散(var関数)の計算
分散は英語ではVarianceといいます。そこで、Rで分散を計算するにはvar関数を使います。
例えば、70~85歳の女性20人の握力測定の結果が以下のようであった場合、
grip <- c(22.1, 17.2, 21.9, 19.6, 23.8, 15.4, 13.2, 15.8, 20.4, 28.8, 25.5, 21.9, 29.2, 19.8, 17.6, 21.4, 25.2, 12.3, 19, 27)
mean(grip)
[1] 20.855
var(grip)
[1] 23.21418
平均:20.855㎏、分散:23.21218となります。
※ここで注意点です。Rのvar関数は「s2(つまり、不偏分散)」を求めています。
もし、母分散(つまり、集めたデータを母集団としてとらえる)を求めたい場合は、
$$\frac{(var関数の値)×(N-1)}{N}$$
で、σ2が求められます。
これで、70~85歳の女性の握力は、平均20.855㎏、分散23.21218ですと言われても、なんだかピンときませんね。
そこで、次に解説する標準偏差(sd)の出番がやってきます。
Rを使った標準偏差(sd関数)の計算
先程、var関数で計算した「握力測定結果」の分散は、元のデータと単位が異なっていることにお気づきでしょうか?
なぜなら、分散の計算において、(実測値ー平均値)2と2乗しているからです。
上の例でいえば、握力の平均の単位は㎏ですが、分散の単位は㎏2となっています。
そこで、元のデータと同じ単位に戻すために母分散(もしくは不偏分散)の平方根をとることでデータの単位を元に戻すことができます。これを標準偏差といいます。
$$σ(母標準偏差) = \sqrt{σ^2}$$
$$s(標本標準偏差) = \sqrt{s^2}$$
標準偏差は英語ではStandard deviation(sd)といいます。Rで標準偏差を計算するときは、sd関数を使います。
先程の握力測定データを使うとすれば、
sd(grip)
[1] 4.81811
となり、握力測定データの標準偏差は±4.81811(kg)ということが分かります。
ここで分散と同様の注意点です。Rのsd関数は不偏分散をもとに計算しています。もし、集めたデータが母集団で、母標準偏差を求めたい場合は、
$$sd関数の値 × \sqrt{\frac{N-1}{N}}$$
とすれば、母標準偏差を求めることができます。
結果、70~85歳の女性の握力は、平均20.855±4.81811(kg)ということが分かりました。
今回はここまでです。
Rのvar関数・sd関数を使った分散と標準偏差についてまとめてみました。



コメント