四分位範囲(IQR: interquartile range)

四分位範囲は、集めたデータ内の「中間の50%」がどこにあるかを示す範囲をいいます。つまり四分位範囲は、値の中央集団がどこにあるかを示す指標ということができます。
四分位範囲は、小さい順に並べられた(昇順)データセットを4つに分割します。各パートを分割する値は、第1、第2、第3四分位と呼ばれ、それぞれQ1、Q2、Q3と表記されます。
四分位範囲を求めるSTEP
STEP1 データを小さい順に並べる
STEP2 何番目のデータが、Q1、Q2、Q3となるかを以下の計算で求める
- Q1 = (deta個数+1)×(1/4)
- Q2 = (deta個数+1)×(1/2)
- Q3 = (deta個数+1)×(3/4)
STEP3 四分位範囲(IQR) = Q3 ー Q1
例題を使って四分位範囲を求める
例えば、以下のような体重データがあったとします。
80.2,80.1,86.4,86.3,76.1,78.1,75.1,86.7,73.5,84.6,77.4,79.5,89.6,81.4,81.8,77.3,84.2,75.4,79.5,73
STEP1:小さい順に並べる
73,73.5,75.1,75.4,76.1,77.3,77.4,78.1,79.5,79.5,80.1,80.2,81.4,81.8,84.2,84.6,86.3,86.4,86.7,89.6
STEP2:Q1,Q2,Q3の順位と値を求める
- Q1 = (20+1)×(1/4)=5.25≒(5位・6位)/2 → 76.7
- Q2 = (20+1)×(1/2)=10.5≒(10位・11位)/2 → 79.8
- Q3 = (20+1)×(3/4)=15.75≒(15位・16位)/2 → 84.4
STEP3: IQRを求める
84.4ー76.7=7.7
となります。
四分位点(25%、50%、75%)以外でも、任意のパーセントの点(=パーセンタイル点)を見つけることもできます。
この場合、
STEP1 データを小さい順に並べる
STEP2 x%が何番目のデータかは
パーセンタイル順位 = (deta個数+1)×(x/100)
で求められます
STEP3 2で求めたパーセンタイル順位の値 = 「パーセンタイル点」
という風に手動で求めることも可能ですが、データ数が増えてくると数えるのも面倒ですね。
Rで四分位範囲を求める
Rで四分位範囲を求める2つの方法を紹介します。
1.quartile()関数 + IQR()関数
x <- c(80.2,80.1,86.4,86.3,76.1,78.1,75.1,86.7,73.5,84.6,77.4,79.5,89.6,81.4,81.8,77.3,84.2,75.4,79.5,73)
quantile(x)
0% 25% 50% 75% 100%
73.0 77.0 79.8 84.3 89.6
IQR(x)
[1] 7.3
2.summary()関数 + IQR()関数
summary(x)
Min. 1st Qu. Median Mean 3rd Qu. Max.
73.00 77.00 79.80 80.31 84.30 89.60
IQR(x)
[1] 7.3
となり、手動で計算したのと若干の誤差はありますが、統計ソフトにより計算方法が異なるため、多少の誤差を気にする必要はありません。
また、データフレーム形式のデータのIQRを求める場合は以下のようにすると簡単です。
最初に、データフレームを作りますね。
y <- c(79.7,80.6,87.3,86,78.1,77.3,77.6,88.3,88.7,84.1,89.4,80.7,78.1,70.5,85.2,78.4,74,91.8,75.1,81.3
)
df.IQR <- data.frame(x, y)
では、
① xのみのIQRを求める
IQR(df.IQR$x)
[1] 7.3
② x、y両方のIQRを求める
sapply(df.IQR[ , c("x", "y")], IQR)
x y
7.30 8.35
(※sapply() 関数は、リスト、ベクトル、データフレームを入力とし、ベクトルまたはマトリックスで出力を行います。リストオブジェクトに対する操作に便利な関数で、sapply 関数はベクトルを返します。)
箱ひげ図について
箱ひげ図は、5数要約(最小値・第1四分位数・中央値・第3四分位数・最大値)を視覚化するのに役立つグラフの一種です。ヒストグラムのように分布についての詳細な情報を理解することは少し難しいですが、
- 5数要約の把握
- データ分布が歪んでいるかどうか
- データセットに潜在的な異常な値(外れ値)があるかどうか
を理解するには便利な図です。
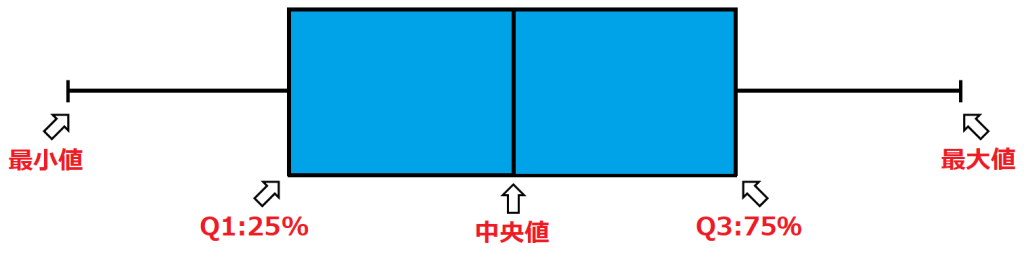
また、箱ひげ図は、中心、広がり、全体の範囲がすぐに明らかになるので、複数の分布を比較するのにも非常に便利です。
手動で箱ひげ図を作図する場合は、上の四分位範囲で求めたQ1~Q3と最大値・最小値を探して、作図すればいいですね。
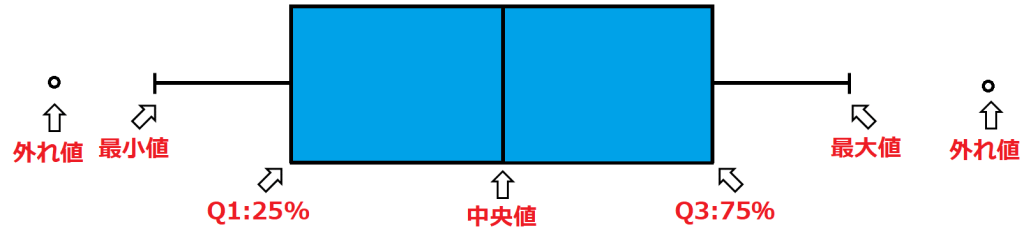
ちなみに外れ値を表記する場合は、ひげの長さを
- 上限:Q3 + 1.5 × IQR
- 下限:Q1 + 1.5 × IQR
として、それぞれの限界値を超えたものを外れ値として示します。
Rで箱ひげ図の作成
Rで箱ひげ図を作成する場合は、boxplot()関数を使います。
最もシンプルに作図するなら、
boxplot(x)
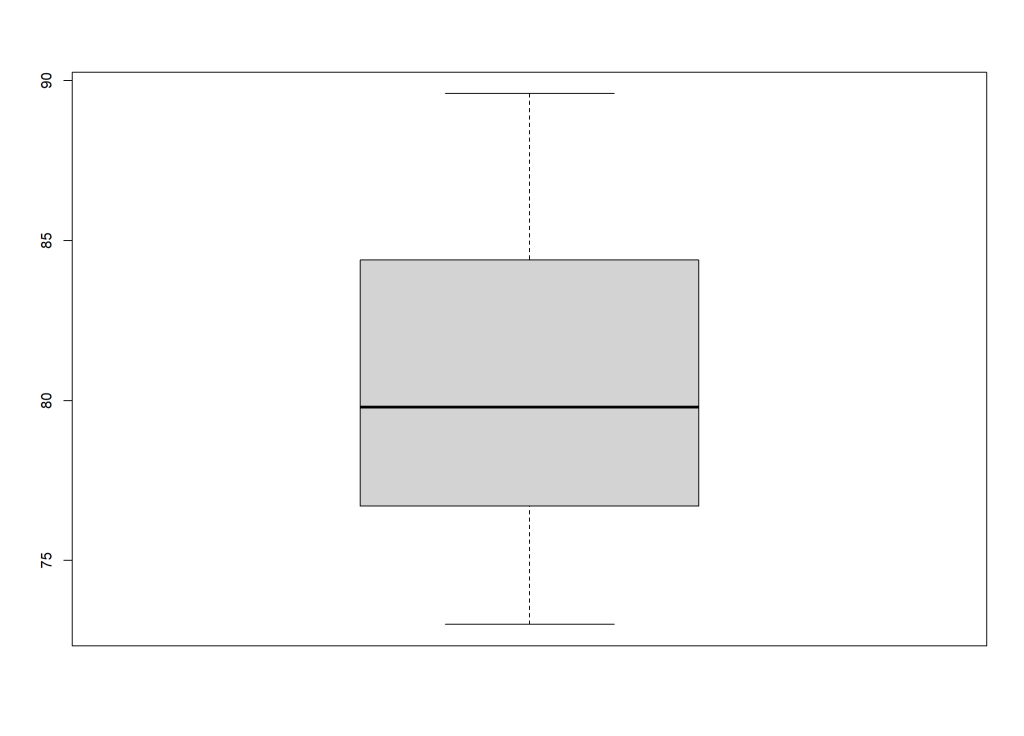
上のグラフでは少し味気ないので、
- x軸のラベル
- y軸のラベル
- 箱の色
- 図を横向き
に変更してみます。
boxplot(x, xlab = "weight", ylab = "x", col = "Orange", horizontal = TRUE)
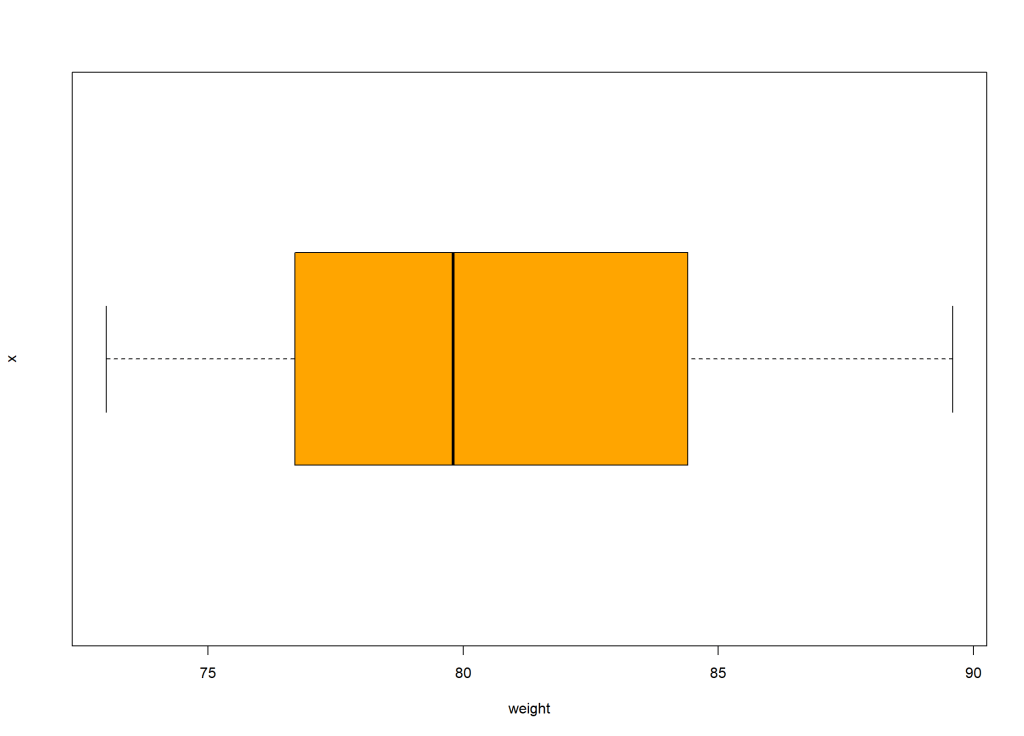
まとめ

四分位範囲と箱ひげ図の作り方をまとめてみました。データを集めた際に、ヒストグラムと一緒にサクサクとRで作図して、データを視覚的に把握するツールとして是非、使ってみてくださいね。




コメント